Abstract: We explain Lamport signatures, a hash based quantum safe digital signature scheme developed in 1979. We use them to illustrate how quantum safe signatures can be very simple and do not require complexity or new maths. We argue that hash based signatures may be the way to go, if Bitcoin is to adopt a quantum safe signature scheme. There is no concrete reason to believe quantum computing poses an imminent or even medium term threat to Bitcoin. However, in our view, the first step in mitigating the apparent quantum risks is giving users the choice of spending Bitcoin in a quantum safe way. Once such a choice is available, the extent of economic user adoption can drive any next steps.

American mathematician and computer scientist Lesslie Lamport
Overview
Bitcoin’s exposure to quantum risk is a hot topic right now. There was even a recent conference in San Francisco, at Presidio Bitcoin, dedicated to this issue. In our view, one should try to be as rational as possible. We do not understand quantum computing and we have not seen any quantum hardware actually achieve anything particularly impressive and therefore it’s probably not worth worrying about. However, we appreciate that the idea is scary to some and that development in quantum technology could in theory happen unexpectedly quickly. One of the general concerns is that Bitcoin might need to update to a new highly complicated and risky post quantum cryptographic digital signature scheme. There are a lot of fancy sounding new schemes one can read about, including HAWK, SQI, Falcon and CRYSTALS. There may be risks associated with the new schemes; what if we select the wrong scheme, in 2023 there were reports that a new post-quantum scheme, the “SIKE algorithm”, was cracked by classical non-quantum means. And what if quantum computing rapidly advances, since barely anyone understands quantum computing, who is to say if these schemes really are quantum safe?
However, if Bitcoin wants to upgrade to a post-quantum signature scheme, we do not necessarily need complicated risky cutting edge technology at all. Remember, Bitcoin’s digital signature scheme, Elliptical Curve Digital Signature Algorithm (ECDSA) is potentially quantum vulnerable, due to a factorisation attack using Shor’s algorithm. Hash functions however, are pretty much quantum safe. Hash functions, like SHA256 are quantum vulnerable based on Grover’s algorithm, which means the security could be reduced by a square root. Therefore instead of 256 bits of security, there would be 128 bits of security. This seems mostly fine and one can always use a hash function with a larger output to increase security if needed.
There are actually signature schemes that rely purely on hash functions. For example Lamport signatures, developed in 1979. This scheme is actually pretty simple, much more simple than the elliptical curve based scheme that Bitcoin uses. And since it relies only on hash functions, it’s quantum safe. Therefore, if Bitcoin adds a quantum safe signature scheme, it does not need to rely on fancy new risky maths, we can just choose a hash based scheme instead. Then Bitcoin could use hash functions for everything, mining proof of work and signatures, making Bitcoin more simple. In the rest of this report we take a look at Lamport signatures and how they work.
How do Lamport signatures work?
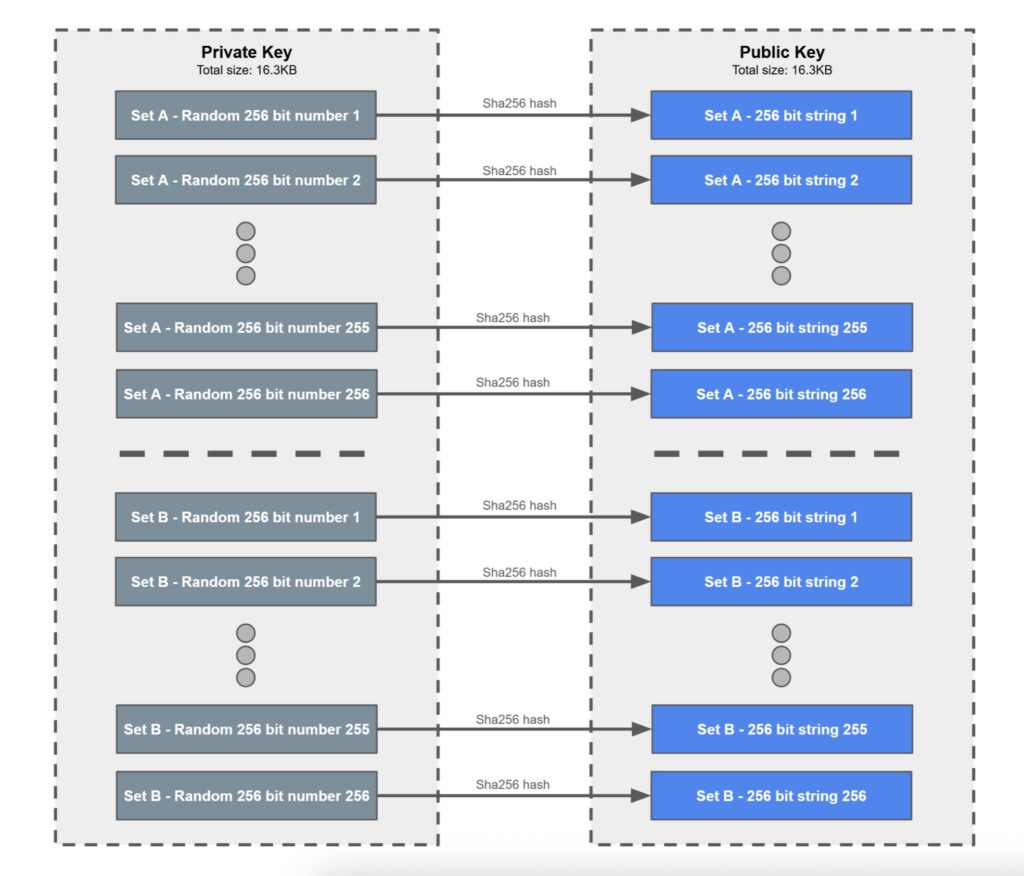
In the below example we assume the Lamport signatures use the SHA256 hashing algorithm, however it can work with pretty much any hashing algorithm. With Lamport signatures, a private key is not just one random 256 bit number like it is with ECDSA, instead its two sets of 256, 256 bit random numbers. The two sets being set A and set B in our example. Therefore, the private key is 2 * 256 * 256 = 131,072 bits = 16.3KB. Each of these 512 256 bit random numbers is then hashed and these output hashes are the public key, therefore the public key is also 16.3KB. A Bitcoin address could then be a SHA256 hash of a concatenation of all the strings which make up the public key. The below images illustrates the private and public key setup.
To sign a message, the first step is to hash the message, again using SHA256 and the output string in binary is produced. Based on each digit of the binary output, this determines which part of the private key is included in the signature. A bit value of zero corresponds to set A, while a bit value of one corresponds to set B. The first bit in the hash output corresponds to the first number in the private key, the second the second and so on. Therefore, the signature consists of a random selection of exactly 50% of the total private key.
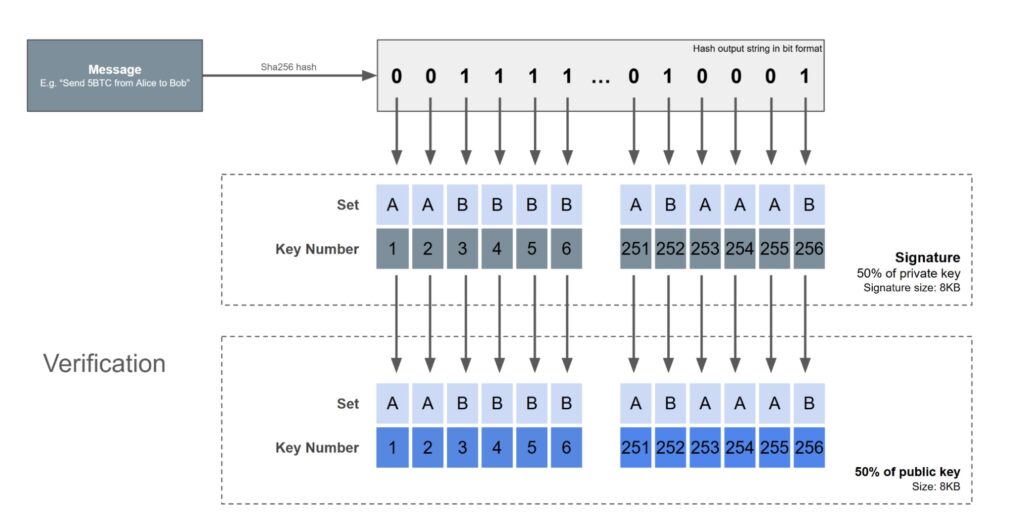
To verify the message, all the verifier has to do is hash the message and select the appropriate parts of the public key using the same methodology. Then the verifier needs to hash each of the numbers in the signature, to see if they match these 256 parts of the public key. If there is a complete match, the signature is valid. The signer needed to know the full private key, since the hash function is random and one could not predict which parts from set A or set B would be needed, until a specific message is chosen. Therefore it is relatively easy to see how this scheme is secure and verification is also computationally pretty straight forward.
One time only
A key weakness with this scheme is that it’s limited to using each signature only once. Once a transaction is signed on the blockchain, 50% of the private key is published. If the signature is used again, then another 50% of the key is published. Statistically, this means 75% of the total private key is now expected to be publicly available. It’s easy to see how the security would deteriorate pretty quickly each time one signs. This means people may not be able to re-use addresses, which is a positive for privacy, however there are some issues here:
- People are accustomed to re-using addresses
- What if someone sends funds to an address that has already been used?
- How would RBF work? There could be an extra input added and only that extra input could be signed, but this creates coin control issues
No clever maths
Another disadvantage is that one cannot do clever maths like one can do with ECDSA. BIP-32 for example, hierarchical deterministic wallets, exploits the characteristics of ECDSA to allow the use of “xpubs”, something that cannot work with just hashes.
Size
Another elephant in the room is the massive size of the signatures and public keys. With a signature being 8KB and a public key being 16KB, this totals 24KB. A Bitcoin block could then only include tens of transactions, rather than the thousands of transactions we have today. However, all quantum safe schemes seem to have this problem to one extent or another.
SPHINCS+
We are only analysing the original basic Lamport signature scheme for illustrative purposes only, just to show how a simple signature scheme that relies only on hashes and is therefore quantum safe, is very possible. If Bitcoin were to add a hash based signature scheme, there are much more modern options available. In 1982, Winternitz published a variation of the Lamport scheme. The Winternitz scheme involved splitting the hash of the message into a number of pieces and mapping these pieces to different parts of the private key; there are then further iterative hashing steps. In 2011, a newer variant XMSS was published and then in 2015, another variant of a hash based signature scheme was published, SPHINCS.
SPHINCS+ can allow for much smaller signature sizes and private keys that can be used multiple times. These schemes involves a Merkle tree structure, with the top of the tree being a “global public key”, therefore typically the public key is just 32 bytes in size. If Bitcoin does adopt a post-quantum signature scheme, it’s these hash based schemes with Merkle trees that may be chosen. Since Merkle trees are already widely used in Bitcoin, it can be seen as convenient to use them here too.
Lightning Lab’s co-founder, Olaoluwa Osuntokun gave a talk about SPHINCS+ signatures at the recent quantum conference in San Francisco. In the talk, he explained how there are several trade-offs one can choose with SPHINCS+, allowing us to achieve the desired characteristics we want depending on our priorities. Parameters that can be tweaked include the hash cost to construct the signatures, the hash cost to verify the signatures, the amount of re-use that is safe and the size of the signatures. Olaoluwa said that the parameters could be set such that signatures could be as small at 2KB, which seems somewhat reasonable. Although of course this is still much larger than current signatures in Bitcoin, which can be around 70 bytes.
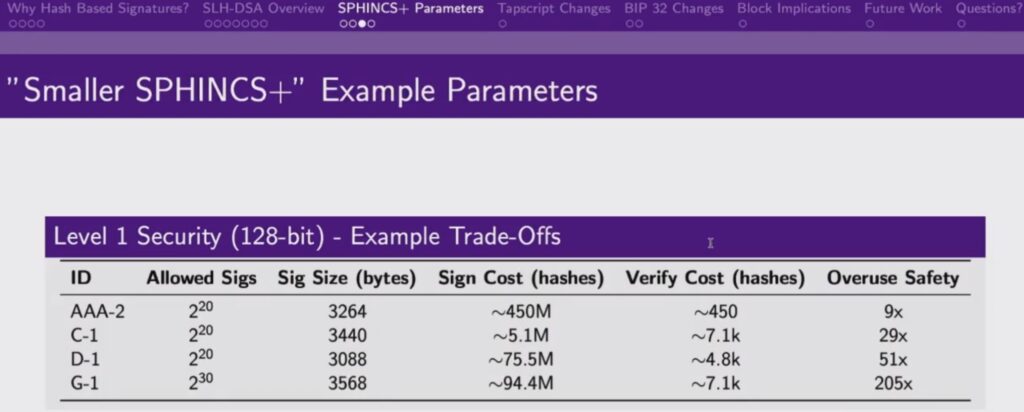
Source: https://x.com/PresidioBitcoin/status/1945877820657508650
Conclusion
We do not have a strong understanding about the level of quantum risk to ECDSA nor do we have anything concrete to go on. In our view it’s very likely that the ECDSA scheme Bitcoin uses is going to be safe for many decades ahead and the rational approach may be to do nothing until we have more concrete examples of the capabilities of quantum computers. However, it may be worth thinking about what it would take to make Bitcoin quantum safe. The first step is creating a way to spend Bitcoin in a quantum safe way, which could be a hash based signature scheme. In our view, there is not much point seriously debating any plan to freeze vulnerable coins until a quantum safe spend option is available and widely used. If a quantum safe way to spend Bitcoin is added and user adoption is strong, only then is it worth engaging in such a debate.
There are of course many issues to work out when it comes to adding a hash based signature scheme. If a new hash based quantum safe signature scheme is added, how will we get adoption given the much larger signature sizes, since these transactions are significantly more expensive? Do we re-visit the blockweight discount and the blocksize limit? Alternatively, we could target economic adoption by value rather than adoption by transaction/UTXO count. Perhaps these quantum safe schemes could be adopted first by entities holding thousands of Bitcoin, like ETF providers or Bitcoin treasury companies, that barely ever make any transactions. To these entities the extra transaction cost would not be significant. Individual users could keep their savings in quantum safe outputs requiring these 2KB signatures, while their day to day spending could be quantum vulnerable. This day to day spending could be made relatively safe by using P2WPKH outputs and avoiding address re-use, if desired. Again using hashes as the quantum defense, with users only at risk while the transaction is unconfirmed.
Once there is considerable economic adoption, it may be easier to talk about the next steps to take in mitigating quantum risks. In our view, once a quantum safe redemption option exists, ultimately the path forward should be led by the economic users. If they don’t use the quantum safe outputs then fine, that is their choice. If adoption is strong, we can potentially move on to talking about other controversial steps, like freezing coins, changing the blockweight limit , BIP-39 seed phrase quantum safe recovery schemes or whatever steps one thinks is necessary. Let the holders decide.
