
Note: This is an article written by Romano RNR – a BitMEX Affiliate and OG crypto trader of 10+ years. You can find the same article on his Medium page here.
Quanto futures are a type of derivative that is measured and paid in a foreign currency before being converted to the domestic currency. They mitigate foreign currency risk.
On the other hand, the inverse futures contracts are designed for ‘bearish traders’ who want to hedge the value of BTC against the U.S. dollar. These contracts work inversely to traditional linear futures; as the price of BTC calls increases, the contract’s value in USD increases, allowing traders to profit from downward market movements.
Maybe you’re not interested in Bitcoin trading, but rather altcoins. If so, you’ll love trading on BitMEX. Please stick with me till the end to apply everything you learn from this article to trade altcoins and supercharge your P&L non-linearly.
Let’s get into the basics first to build a foundational understanding.
Ever thought about buying property in another country?
It sounds like a great side hustle, but there’s a catch. There are multiple, but this one is often overlooked.
Investing in property abroad means you’re not just dealing with bricks and paperwork.
You’re playing the currency game whether you like it or not, and that game is tricky.
Even if your overseas property is doing great, currency fluctuations can turn massive profits into losses when you bring your money back home.
You’re probably wondering where I’m going with this and how it relates to quanto futures, but it will make sense.
Imagine you’re from the U.S., and you buy property in Japan. Without protection, if the Yen takes a nosedive against the dollar, your investment might do the same, even if the property itself is worth more Yen than before.
So, imagine you’re an investor from the United States and decide to buy property in Japan. You convert your U.S. dollars (USD) to Japanese Yen (JPY) to purchase the property.
If 1 USD equals 100 JPY, your property investment costs $1m. Calculated as 100 million Japanese yen divided by 100 JPY per US dollar.
100,000,000 / 100 = 1,000,000
Let’s assume the value of your property increases over time, and now it’s worth ¥120 million. In terms of Yen, your investment has increased by 20%.
But the yen and dollar exchange rates changed while your property’s value increased.
Suppose the Yen weakened against the dollar, and now $1 = ¥120
Now, you decide to sell your property for ¥120, but when you convert it back into the dollar, you’ll get $1m.
120 million JPY / 120 JPY per USD
Despite your property gaining 20% value in Yen, you will not make any profits when you convert back to dollars.
This shows currency (FX) risk. While your investment did well in the local currency (Yen), the change in the currency rate (Yen) depreciating against the dollar neutralized all your gains when you converted it back to the home currency (dollars).
Let’s say you’re an investor from the good old United States of America and have your eyes on some real estate in Europe. You want to drop some of your green bags (dollars) on it.
Disclaimer: It is possible that there are mistakes in this article and the code on GitHub. This article was a lot of work. Please provide feedback and, if possible, a GitHub pull request to improve or fix it.
Yet again, you’re playing 2 games at once.
The property game and the currency game.
You’ve got your property moving in value and have the euro fluctuating against the dollar. The value of your European property could go up, but if the Euro decides to take a nose dive against the dollar, things are getting more complicated.
Now, we have a fancy formula.

\begin{align*}
\frac{(V_1 - V_0)}{V_0} &= \left\{ \frac{[V_0 \times (1 + r)] \times [1 + fx] - V_0}{V_0} \right\} \approx r + fx, \\
\text{where} \quad & V_0 \text{ is the current value of the property in euros,} \\
& V_1 \text{ is the value of the property in the next period,} \\
& r \text{ is the percentage change in the property value in euros,} \\
& fx \text{ is the percentage change in the value of euros expressed in terms of US dollars.} \\
& \text{The equation is an approximation because it ignores the cross-product } r \times fx. \\
& \text{The scale of the investment (i.e., €100 million) is irrelevant to the return } R.
\end{align*}.
This formula can tell you how much “bang for your buck” you’re getting after the dust settles. Now, let’s go over this first without going into the maths of the formula and explain it.
If the Euro appreciates against the dollar, you’re in luck. You’re making extra money on top of whatever the property is making.
If your European property’s value jumps up by 3% while the Euro appreciates against the dollar by 5%, you’re not just up by 3%, but you’re up 8% when you convert those euros back to dollars.
Considering the property’s performance and the Euro, this shows you how much cash you could pocket in dollars.
Dealing with international property investing is more than just putting up that “For Sale” sign; it’s also about the currency game.
Now, Let’s Get into the Details of the Maths
This equation estimates the return an investor can expect from an investment. It takes into account the change in the asset’s value in local currency (r) and the change in the exchange rate (f𝑥).
To explain it in our example:
Let’s assume a US investor is interested in a European property valued at €100 million. In this scenario, the investor is concerned with the changes in the property’s value and the Euro’s value against the US dollar. The European property is appreciated from €100 million to €103 million.
In academic jargon, this phrase would be included in research papers on finance.
For example, to the US investor, a property with a current worth, V_0, of €100 million can be viewed as having a return R, based on the next period value V_1, as shown in this equation:
(V_1- V_0)/V_0 = {[V_0 * [1 + r] * [1 + fx]] – V_0 ≈ r + fx
I will make the equation more readable with LaTeX.
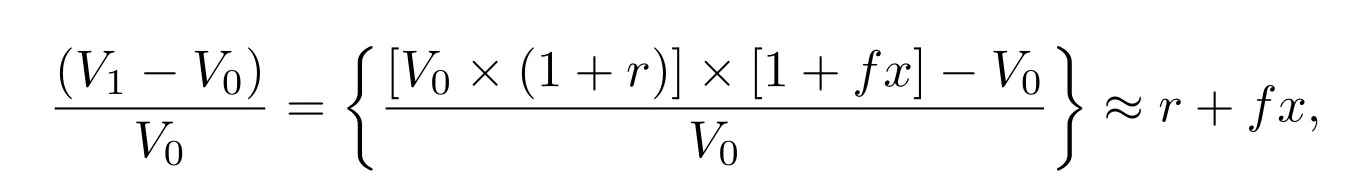
Equation 40.1
Note phrase:
“V_0, of €100 million can be viewed as having a return R, based on the next period value V_1”
V_0 is €100 million, and V_1 is €103 million, yet we don’t know “r” yet. So, let’s figure that out.
The total percentage gain or loss in the value of the total investment is denoted by “r,” which tells us how much our investment is worth compared to when we first invested.
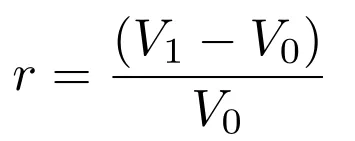
We need to find out how much the property’s value changed if we bought it for €100 million and it’s now worth €103 million. The change in value (€103M — 100M) is €3 million.
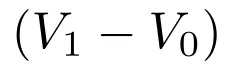
€103 million — € 100 million = €3 million
Next, we want to see how this change is relative to what we paid, so we divide the €3 million by the original €100 million.
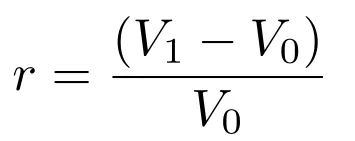
(103 million — 100 million) / 100 million
In this case, dividing €3 million by €100 million gives us 0.03, but to turn this into a percentage, we multiply by 100, which gives us 3%.
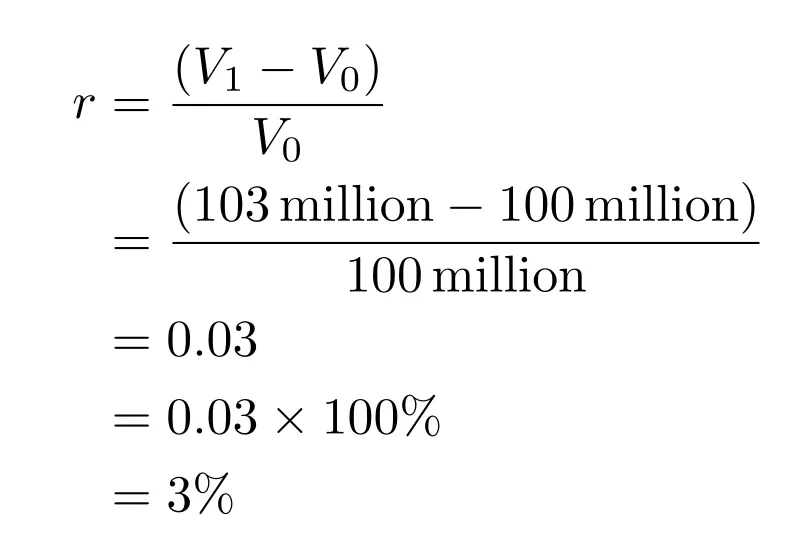
Did you waste my time reading to give me a basic explanation of how to calculate the percentage gains/losses? Yes, yes, I did.
We have confirmed that our gain on the property is 3%.

Suppose we are a US investor buying European property at €75 million with our dollars. We are hoping for a 4% increase in the property’s dollar value over the year.
Let’s simplify the math and assume €75 million is worth $100 million. We purchased this European property worth €75 million and paid $100 million.
What happens to our dollars if the Euro appreciates or depreciates against the dollar?
Scenario 1 (Euro Appreciates):
- Property value up 4%
- Property value: 75 * (1 + 0.04) = €78M
- Euro appreciation: 2%
Now, to find the “Next-period property value in dollars” denoted as P_next:

In our case:

By plugging in the numbers, we get:
P_next = (75 × (1 + 0.04)) × ((100÷75))×(1+0.02) = $106.08M
Scenario 2 (Euro Depreciates):
- Property value increase: 4%
- Next-period property value: (€75M * 1.04) * 0.98 = €76.44M
- Euro depreciation: -2%
- Next-period property value in dollars:
Now, to find the “Next-period property value in dollars” denoted as P_next:

In our case:

By plugging in the numbers:
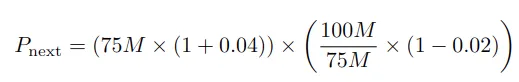
P_next = (75×(1+0.04)×(100÷75)×(1−0.02)) = $101.92M
So, you managed to purchase property overseas, and even if the local price of the property doesn’t move, the value back home can swing just due to the currency exchange rates.
You’ve bought your property in Europe, and the Euro might fall against the dollar (EUR/USD down), and suddenly, your property isn’t worth as many dollars as before.
Your investment worth in your “home currency” (let’s say dollars) can jump around even if the price of your property in the “local currency” (let’s say Euro) has stayed the same.
It’s not just about property value. It’s also about the foreign exchange game you’re participating in. Without heading, you’re pretty much partly gambling.
Key traditional currency risk assumptions of cross-border investing
When investing in real estate across borders, it’s important to be aware of currency risk since you’re indirectly playing the foreign exchange market.
A common belief in currency risk management is that fluctuations in the value of the investor’s home currency can influence the value of their foreign investment.
This means that if the currency in the country where you have invested (for example, the Euro) strengthens or weakens against your home currency (for example, the US dollar), it will affect your returns.
For instance, if an American investor’s European asset appreciates by 4% in USD terms, traditional wisdom suggests this is independent of the USD’s market performance. That viewpoint implies that owning foreign assets inherently involves currency risk.
However, this might not hold in significant currency devaluation or inflation scenarios.
In such situations, the nominal value of real assets, when calculated in the inflating currency, tends to mirror the high inflation rate.

\begin{align*}
\frac{(V_1 - V_0)}{V_0} &= \left\{ \frac{[V_0 \times (1 + r)] \times [1 + fx] - V_0}{V_0} \right\} \approx r + fx, \\
\text{where} \quad & V_0 \text{ is the current value of the property in euros,} \\
& V_1 \text{ is the value of the property in the next period,} \\
& r \text{ is the percentage change in the property value in euros,} \\
& fx \text{ is the percentage change in the value of euros expressed in terms of US dollars.} \\
& \text{The equation is an approximation because it ignores the cross-product } r \times fx. \\
\end{align*}
Remember the equation above, which helps us understand the combined effect of the property’s value change and the currency exchange rate on your investment’s overall value.
So picture this: you’ve got a property where the local currency, say the Euro, is taking a nosedive compared to the US dollar. In finance, we’d expect the return of the property (that’s our friend “r” in Equation 40.1) to mirror this.
When investing in properties across different countries, you’re playing a dual game of real estate and foreign exchange markets. Here’s where Equation 10.1 becomes relevant.

Equation 10.1
\begin{equation}
\sigma_p = \frac{\partial \sigma_p}{\partial w_1} w_1 + \ldots + \frac{\partial \sigma_p}{\partial w_N} w_N
\end{equation}
Where:
\begin{itemize}
\item $\sigma_p$ is the standard deviation of the portfolio's returns, representing total risk.
\item $w_i$ is the weight of the \(i^{th}\) asset in the portfolio.
\item $\frac{\partial \sigma_p}{\partial w_i}$ is the partial derivative of the portfolio's standard deviation with respect to the weight of the \(i^{th}\) asset, representing how sensitive the portfolio's risk is to changes in the weight of the \(i^{th}\) asset.
\item The summation runs from 1 to \(N\), where \(N\) is the total number of assets in the portfolio.
\end{itemize}
This equation helps us determine how our whole investment is based on the risk of each investment (like properties and currency holdings) and how much of our money is in each part.
In real case scenarios, if the currency in which an investment is made devalues significantly, say by 25%, the property’s value in that currency may increase substantially.
This helps to maintain the property’s real value. Traditional models often overlook this possibility.
It’s not just about the property’s price tag; it’s also about how currency values and economic conditions in the investment country can affect your returns.
Accessing foreign assets with futures and Quanto futures
In finance, equity futures contracts are financial instruments where investors agree to buy or sell a specific stock index or individual stock at a predetermined price on a future date.
I assume the reader has a basic understanding, but let’s review it just in case.
Equity futures are contracts you make with someone to buy or sell stocks at a set price on a future date. You don’t actually get the stocks; you settle the bet with cash. Traders use these contracts to protect against risks or to try to make money from expected price changes. They’re useful because you can trade a lot with a little bit of cash with leverage.
So, at expiration, the buyer and seller settle the difference between the contract and market prices in cash. There’s no physical exchange of the actual stocks or indices. On the other hand, oil futures often involve physical delivery.
(Remember during the COVID pandemic, when oil futures ended up trading negatively because almost nobody wanted physical oil delivery at their door).
These contracts are generally linked to the performance of indexes such as the SPX500. They are traded in the currency of the underlying assets. For instance, if the futures contract is based on the SPX500 index in the U.S., it would be traded in U.S. dollars.
How does that work? It’s quite straightforward.
Each contract has a specific dollar value assigned to each point movement of the index. Consider a contract valued at $250 per point. If the SPX500 index rises by 2 points, a market participant holding a “long” position (bet on the index rising) would gain $500.
That profit is calculated as:
contract value * points = PNL
$250 * 2 = $500
A Quanto derivative takes this concept a step further.
What Are Quanto Futures?
Do you Quanto? Have you ever heard about quanto derivatives? Quanto products are a type of derivative that gained popularity over the years due to their ability to mitigate foreign currency risk.
Quanto products, known as “currency-linked derivatives,” were originally developed in the late 1980s to meet the demands of investors who wanted to participate in the explosive rally in Japanese stocks and avoid the risk associated with fluctuations in the Japanese Yen.
During the late 1980s, the popularity and acceptance of quanto products led to the rapid globalization of financial markets. These financial instruments were designed to effectively manage cross-border investment risk by providing investors with exposure to foreign assets without exposing them to the risks associated with currency fluctuations. This innovation was a significant development that helped to improve and streamline international investment activities.
It’s a type of financial derivative where the payoff is adjusted based on a certain quantity, usually involving a foreign exchange rate. In essence, quanto derivatives combine the speculation of the price movement of an asset with the potential fluctuations in exchange rates.
These products are designed to have their payouts in a domestic currency, even though the underlying assets are priced in foreign currencies. They ensure that no matter what currency your investment is in, you get your returns in your home currency.
Let’s say you’re an American investor; Quanto products allow you to invest in foreign assets with your dollars without worrying about the currency exchange rate of the foreign currency you’ve invested in.
Who coined the term “Quanto derivatives”, and where did this “Quanto” originate from?
Now, it’s worth asking, “Who came up with this genius idea?” Well, as far as I know, it’s a mystery. The term “quanto” is believed to have first appeared among a team of traders at Salomon Brothers. Salomon Brothers was famous for creating new ways to manage currency risk. At Salamon, they used “quanto” to describe derivatives linked to foreign currency indexes.
The story originated from a hopeful interviewee drenched from a 6-block walk and walked into Cooper Neff’s office in Philadelphia. Cooper Neff was a renowned proprietary trading firm known for its innovative strategies in options trading and other financial derivatives. They were also known for their grueling, rigorous interviews.
During the interview, the candidate was presented with a challenging question that included Siegel’s Paradox.
The question was something like this: The USD/DM (U.S. Dollar/German Deutsche Mark) exchange rate is 1. It has a chance of rising to 1.50 or dropping to 0.50 with equal probability. What’s the fair value?
Simple math suggests the fair value is 1.00 USD.
Now, let’s flip or invert it to DM/USD. The rate could either hit 0.67 (1/1.5 = 0.67 ) or soar to 2.00 (1/0.5 = 2). When you average these out, you get an expected value of 1.335 DM, suggesting a fair value of 0.75.
What gives?
The fair value is the average of the two possible future rates. Since the average (expected value) is 1 DM per USD, the fair value under the given assumptions and market conditions is also 1 DM per USD.
Let’s go over the math a bit.
USD/DM
Current rate: 1 USD = 1 DM
Possible future rate: 1.50 DM
Possible future rate: 0.50 DM
USD/DM Expected value: (1.5 DM + 0.5 DM) / 2 = 1 (straight forward)
Fair value: (1.50 + 0.50) / 2 = 1
Note: Fair value is average of the two possible futures rate
DM/USD (inverted)
1 USD = 1.5 DM
Possible future rate: 1 / 1.50 ≈ 0.67 DM/USD
Possible future rate: 1 / 0.5 ≈ 2 DM/USD
DM/USD Expected value: (0.67 USD + 2 USD) / 2 = 1.335 USD
Note: To determine the fair value of USD/DM
Calculate the expected value of DM/USD by inverting the 1.335 USD
Fair value DM/USD: 1/1.335 ≈ 0.75
Now, someone new to trading may wonder, “What? How can the same currency pair have two different values?”
I understand where the insight came from. This is not a paradox but just a matter of perspective. USD/DM and DM/USD represent the same relationship differently. They are not separate but just different units of measurement. This means that the rates are priced in different units. Therefore, there is no actual inconsistency or trading opportunity.
There is no financial opportunity for purchasing power arbitrage, so there is no real paradox; the difference comes from how we mathematically interact with these rates, and there is no “free lunch.”
When looking at currency rates, we found that complex math is sometimes misused in finance. This includes misusing concepts like Jensen’s inequality, which can lead to misunderstandings in financial theories and practices. In our case, when we averaged rates like USD/DM and DM/USD and converted them, we applied a non-linear function.
We calculated the expected value by taking the average of future rates and then finding its inverse through division, which involves non-linear transformation.
Fast-forward a few years. The Chicago Mercantile Exchange (CME) introduced innovative currency cross-rate contracts priced in USD, like DM/JPY. This was an interesting development but didn’t quite take off as hoped.
However, we are familiar with the Base and Quote currency.
What are the Two Main Types of Quanto?
There are two main types of quantos: two-currency quantos and single-currency quantos.
The Two Currency Quanto: Imagine you’re investing in something priced in euros, but you want your return in dollars. This type is initially valued in euros. When it’s time to cash in, it’s converted into dollars. For this type, where conversion into the domestic currency happens, the pricing tends to be more straightforward. That’s because the conversion rate is known in advance, making it easier to calculate the payoff.
The Single-Currency Quanto: This one is a bit different. Let’s say you’re in the Japanese stock market and eyeing the Nikkei Index. With a single-currency quanto, even though your investment tracks the Nikkei, you’ll get your payout in your good old dollars. No conversion is needed. This type of pricing is more complex, where the payout remains in the domestic currency without any conversion. In this case, the pricing model takes into account any potential fluctuations in exchange rates during the contract’s life.
Quanto options basic
Take quanto options, for example. This is a special type of option contract where the payoff is converted into a different currency at a predetermined exchange rate. Unlike regular options, which pay off in the currency of the underlying asset, quanto options allow investors to receive payoffs in a currency of their choice, using a fixed exchange rate agreed upon at the contract’s inception.
- Currency conversion: Quanto options are an effective way for market participants to gain exposure to foreign markets without being exposed to the associated currency risk. These options provide payoffs in a currency different from the underlying asset’s currency.
- Fixed exchange rate: When entering into a contract, the exchange rate used to convert the payoff from the underlying asset’s currency to the chosen currency is determined and fixed. This fixed rate remains the same regardless of any changes in the market exchange rates at the time of payout.
- Floating-rate quanto options have no predetermined exchange rate. They offer investors flexibility but also expose them to currency risk. Instead, the exchange rate used to convert the payoff is determined at the time of settlement.
- Hedging against currency risk: Quanto options allow investors to hedge against fluctuations in currency exchange rates by locking in the exchange rate.
- Payoffs in preferred currency: Investors have the flexibility to receive payoffs in their preferred currency, which can be more convenient as it aligns with their risk management.
A quanto option is different from a regular option in that it converts the payoff into a different currency using a fixed exchange rate set at the contract’s start. In contrast, a regular option has a straightforward payoff in the underlying asset’s currency.
Imagine a regular option that pays out $4 at the end of its term. Imagine a quanto option with the same underlying asset and conditions but a different way of handling the payoff.
In a quanto option, the $4 payout is converted to euros, but not at the current market exchange rate. Instead, it is adjusted to a predetermined exchange rate, for example, $1.25 per Euro.
In a quanto option, the payout of $4 is converted to euros, but not at the current market exchange rate.
Instead, it is adjusted to a predetermined exchange rate, for example, $1.25 per Euro. It is important to note that the $4 payout is not directly converted to euros at the $1.25 per euro rate stated in the terms.
Rather, the payout is converted to an equivalent value in euros, meaning the investor receives 4 euros. If you convert 4 euros to dollars using the predetermined exchange rate of $1.25 per Euro, it would equal $5.
4 * 1.25 = 5
Instead of a $4 return, it now equals a $5 return.
- The math for quanto options is more complex than for regular options because it involves two currencies and an FX risk premium.
This mechanism offers a unique advantage. It shields the investor from the unpredictability of exchange rate fluctuations.
In another case, imagine the dollar depreciates 10% against the Euro, meaning that if the current exchange rate were $1.10 per Euro, it would shift to $1.21 per Euro.
1.10 * 1.1 = 1.21
If an investor holds a non-quanto fixed-rate investment at $1.25 per Euro, any dollar depreciation will affect the returns when converting to euros.
Despite the exchange rate fluctuating to $1.21 per Euro, the Quanto derivative with a fixed rate remains anchored at the predetermined $1.25 per Euro, making it unique. This means the Quanto contract’s investor is protected against unfavorable market fluctuations caused by foreign exchange movements.
Let’s look at a practical example to understand this better. If the quanto derivative results in a payoff of 10 euros with a floating rate under normal circumstances, this would be converted into dollars at the prevailing market rate.
Given the dollar’s 10% depreciation, the investor would normally receive $12.10 (10 euros * 1.21 per Euro) instead of $11 (10 euros * $1.10 per Euro) before the depreciation.
However, with the quanto contract’s fixed rate of $1.25 per Euro, the investor still receives $12.50 (10 euros * $1.15) despite the shift in foreign exchange.
By locking in the exchange rate from the outset, the investor’s return is influenced by the underlying asset’s performance and the predetermined exchange rate.
Quanto derivatives offer a sophisticated way to hedge currency risk while allowing investors to tap into foreign asset markets.
How Do Quanto Futures Contracts Work?
We are all familiar with futures contracts. Futures contracts are commonly known agreements that allow parties to buy or sell a stock index at a predetermined price on specific dates. These contracts can be utilized to hedge or speculate on the price of a particular asset.
Futures contracts allow investors to manage risk and maximize returns. They can hedge investments to protect against price fluctuations or speculate on an asset’s price to profit from them.
In a Quanto futures contract, the underlying asset is usually priced differently than the investor’s home currency. For example, a Quanto future contract in the U.S. might be based on the Euro Stoxx 50 index, which is denominated in euros, but the contract’s payouts are in U.S. dollars.
In a Quanto futures contract, the exchange rate is determined and locked in when the contract is created. This rate stays the same throughout the contract’s life.
This fixed rate calculates the value of gains or losses in the underlying asset, such as a stock index, in the currency used for contract settlement.
Imagine you’re in the U.S. and enter a Quanto futures contract based on a European stock index like the DAX, measured in euros.
The fixed exchange rate for this contract is set at 1.2 USD for every euro.
If the DAX goes up by 100 euros, you would normally expect to get the equivalent of that increase in your own currency (USD). Still, with a quanto futures contract, this 100 euro gain is automatically converted into USD at the fixed rate of 1.2, regardless of the current market exchange rate. So, you’d get $120 (100 euro * 1.2)
If you opt for a quanto future trade, you can lock in the exchange rate at 1.2 and receive payment in dollars, even if the euro decreases in value against the dollar.
For example, if the EUR/USD exchange rate falls by 10%, you will still earn $120 on your trade. However, if you were trading a non-quanto future, you would still earn 100 euros, but the dollar value would be 10% less due to the decline in the EUR/USD exchange rate. So, instead of earning $120, the 100 euros would only be worth $108.
By trading quanto futures, you know exactly how foreign gains or losses will translate into your own currency, eliminating the uncertainty of exchange rate fluctuations.
So, in a regular scenario, you face two risks if you trade the Euro Stoxx 50 index, DAX, or Nikkei 225. The index performance risk and the currency exchange risk. The fixed exchange rate neutralizes the currency risk in Quanto futures. Your payoff is still linked to the foreign asset but converted into your local currency using this fixed rate.
You’re no longer exposed to the risk of currency fluctuations; your risk is now purely based on the asset’s performance, adjusted by a fixed currency rate.
How Does a Quanto Futures Multiplier Work?
Notably, most futures contracts are “quantity-adjusted” and use “multipliers” to adjust for the quantity.
A contract’s settlement has a multiplier. For example, a wheat future contract might represent 5000 bushes of what, or an S&P500 future contract might be 250 times the index value.

These multipliers merely scale the size of a single contract to a convenient level. In simpler terms, multipliers make the size of the contract more practical and sizable for trading. They don’t change the fundamental nature of the risk.
Quanto futures contracts also use a form of quantity adjustment, but it’s different. Instead of adjusting the physical quantity of size, they adjust the payoff using a currency exchange rate.
For instance, in a Quanto futures contract based on the Nikkei 225 index, the gains or losses in the index are converted into another currency, like USD, using a predefined exchange rate.
For example, if a Quanto futures contract is based on the Nikkei 225 index but settles in USD, and the fixed exchange rate is 0.009 (meaning 1 Japanese Yen equals 0.009 USD), then 0.009 acts as a multiplier that determines how much a gain or loss in Yen is worth in USD.
As explained earlier, Quanto Futures contracts take it a few steps further. Quanto futures are a type of financial derivative that combines elements of futures contracts with currency exchange rates.
Quanto Futures stands out from other futures contracts due to its exceptional feature of including currency exchange rates in the contract. This means that the contract’s performance is not solely dependent on the underlying asset, such as a stock index, but also on the fluctuations in an exchange rate.
To Quanto or Not to Quanto? Does the Perfect Hedge Exist?
The idea of the “perfect hedge” is to protect your investment from losses by managing your position size and protecting yourself against price or currency changes.
However, this ideal is not the reality for most portfolio managers, who tend to keep the share quantity fixed. Instead, they only adjust their hedge against currency changes.

This approach, unfortunately, leads to a “slippage,” where the portfolio, though nominally “fully hedged,” still faces some risk exposure.
The process of achieving a perfect hedge can be challenging, especially when using quanto hedging.
- Dealers and market makers often demand a “risk premium”. This extra cost compensates for potential slippage and errors in their hedge.
- Moreover, transaction costs and fees can deter frequent adjustments for perfect hedging.
- Market dynamics, such as shifts in the underlying asset or exchange rates.
- The unpredictable correlation between asset prices and exchange rates.
Some traders may opt to accept the imperfections of their hedge, such as forward hedging, instead of paying the premium for a quanto hedge.
Forward contracts don’t require a premium, which may be an advantage. However, this is usually canceled out by slippage, and the hedge won’t perform as expected. For those who care about risk, paying for a fairly priced quanto might be a better choice.
This topic may need a separate article. I may add additional information here later.
Crypto Quanto Futures Contracts
Quanto futures are fascinating, and understanding the mechanics behind futures contracts, especially those of quanto futures, is important for novice and seasoned traders.
Let’s start with understanding how to calculate the value of Bitcoin (XBT) and US Dollar (USD) in a BitMEX quanto futures contract, making these complex financial concepts understandable to everyone.
A Bitcoin quanto futures contract allows traders to speculate on the price of Bitcoin in terms of USD, but the contract itself and the eventual settlement are in Bitcoin.
So, the payout of these quanto contracts is in a different currency than that of the asset’s pricing currency, adding a layer of speculation and hedging potential.
If you want to signup to BitMEX and want a 10% discount. You can use my referral link: https://www.bitmex.com/app/register/vhT2qm
Understanding the Multiplier in BitMEX Quanto Futures contracts
When trading Quanto futures, the one term that often pops up is the “multiplier.” Although it may sound complex, it is actually a straightforward concept that plays an important role in determining the value of your bet on Bitcoin (XBT) and US dollars.
What is a Bitcoin Quanto Future Multiplier?
In the context of a BitMEX quanto futures contract, the multiplier is a specific number that helps convert the contract price into the actual value that traders work with. Think of it as a secret ingredient in a recipe that determines your final contract value. In the case of BitMEX quanto futures, this multiplier is set to 1000 Satoshis or 0.00001 BTC.
I know what you’re thinking right now. Why use a multiplier at all? The answer lies in the way futures contracts are structured. The multiplier allows traders to engage with contracts without directly dealing with the full price of Bitcoin.
It essentially “scales” the contract to manageable levels, making it more accessible for traders. This is important when prices can be highly volatile, and the full price of a single bitcoin might be prohibitively expensive for individual traders.
How does the BitMEX Quanto Multiplier Affect Contract Values?
Using our given multiplier of 0.00001 BTC, let’s determine the values of BitMEX quanto futures contracts. This multiplier is applied to the contract price and the number of contracts to calculate the contract’s value
- For Bitcoin Value (XBT value), the calculation is straightforward: we multiply the contract price by our multiplier (0.00001 BTC) and then multiply by the number of contracts (10,000 in our example). This tells us how much the Bitcoin contract is worth
- The process is slightly different for USD value (USD value) but still relies on our multiplier. We square the contract price, then multiply by the multiplier and the number of contracts. This calculation gives us the contract’s value in USD.
Our formulas
Bitcoin value = contract price * multiplier * number of contracts
USD value = price * multiplier * number of contracts
Let’s apply what we’ve learned with this example for a contract priced at $100
- XBT value = 100 * 0.00001 * 10,000 = 10 BTC
- USD value = 100² * 0.00001 * 10,000 = $1000
We can graph our PNL for the price of Bitcoin $0
The calculations start simple; both XBT and USD values begin at 0, as there’s no contract price to multiply.
When the XBT value is $50, it reflects a direct linear relationship with the contract price and is represented by 5 BTC. However, the USD value jumps to $250 due to the contract price’s squaring.
When the Bitcoin value reaches $100, it doubles to 10 BTC. However, the USD value quadruples to $10,000, showcasing the quadratic increase.
Source code for the python script to generate this graph: https://github.com/romanornr/bitmex_pnl_model/tree/main/inverse_futures
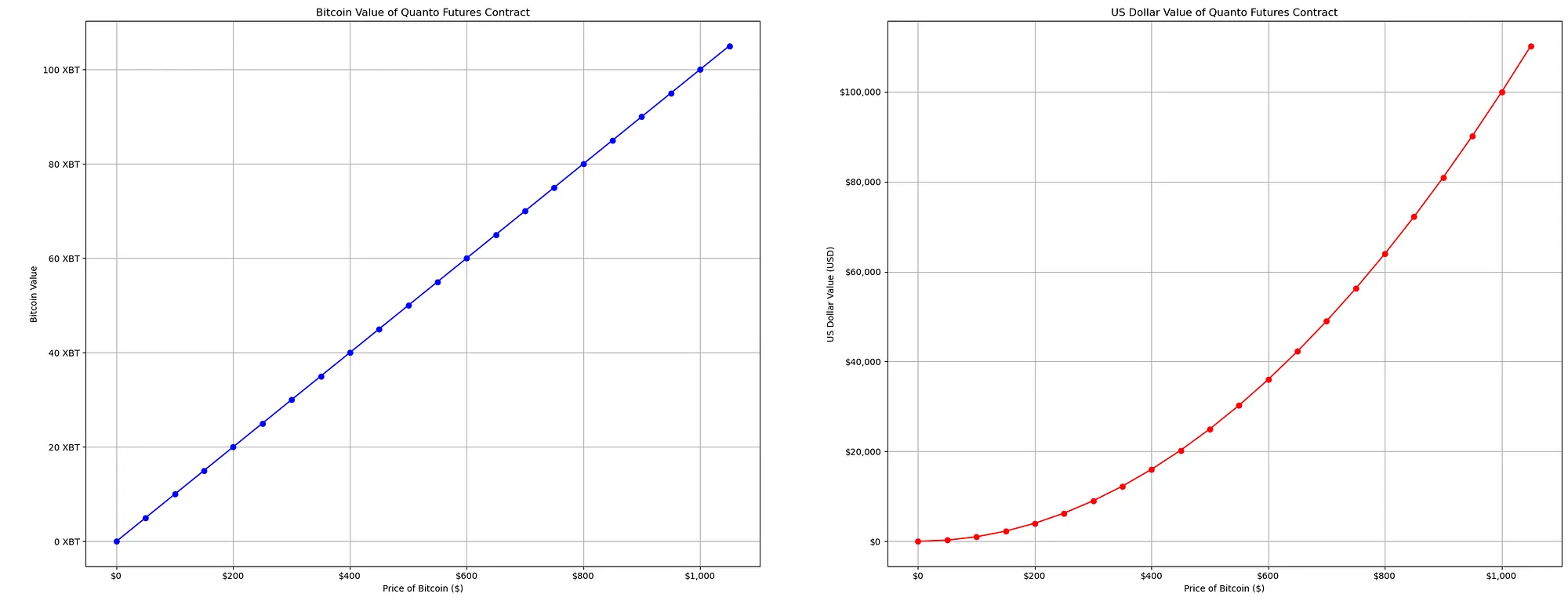
At $1000, Bitcoin’s value reaches 100 BTC, and the USD’s value skyrockets to $100,000, highlighting the exponential growth in dollar terms.
Here’s the video I used from BitMEX to write this article: https://www.youtube.com/live/0d1oITE3jDI?si=oMw2CfahRZQtUX9b
I didn’t use their Excel sheets; I just created some Python scripts that can be modified for specific contracts that may differ, such as Ethereum.
Disclaimer: For demo purposes and to align with the correct calculations of BitMEX’s Excel sheet, I’m using Bitcoin for Quanto futures. However, they don’t have them for Bitcoin anymore, but they do have them for altcoins. The specs of the contracts are slightly different, so the Python script has to be modified.
BitMEX has many Quanto futures contracts for altcoins such as Ethereum, BNB, SUI and many others. You can find them here: https://www.bitmex.com/app/contractList#Quanto-Futures
What are BitMEX Bitcoin and Altcoin Inverse Futures?
In traditional trading, most contracts you come across are straightforward. When you buy one of these contracts (let’s say BTC/USD), how much you could gain or lose stays the same no matter the Bitcoin price. If you enter a trade and later exit, your profit or loss is just the difference between the buying and selling price.
However, an ” inverse ” contract is a different kind of contract. Though it still deals with Bitcoin/USD, its workings are flipped. Instead of your contact’s value being fixed in Bitcoin, it’s fixed in dollars.
BitMEX’s inverse futures contract provides that. These contracts provide a fixed value in US dollars tied to the fluctuating price of Bitcoin. What’s great about them is that they are easy to understand. To calculate their value, you multiply the dollar value of the contract by the number of contracts you own.
BitMEX offers a type of derivative called the XBTUSD Perpetual contract, which is an inverse futures contract. The value of this contract is linked to the XBT/USD exchange rate, which is tracked by the BXBT index. Though both the underlying asset and the swap contract are priced in USD, margins, and PNL are measured in Bitcoin.
Here’s how this contract is structured:
- The multiplier is set at $1
- Find the XBT contract value, which you do by taking the multiplier and divide by the XBTUSD price
- The USD contract value is $1
- PnL is calculated using the formula: Number of contracts * Multiplier * * (1/Entry Price – 1/Exit Price)
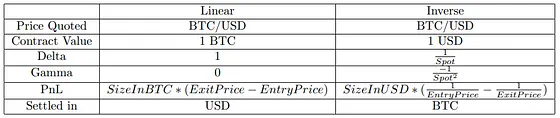
PNL is realized in BTC, which avoids interaction with USD.
When dealing with BitMEX inverse futures contracts, your profits or losses are not fixed in Bitcoin but in US dollars. The contracts are set up to maintain a constant dollar value regardless of the Bitcoin price. In terms of potential financial returns, these contracts provide a consistent amount in US dollars but yield an exponential return in terms of Bitcoin.
I know this sounds vague, but don’t worry. I will try to break it down.
No matter the bitcoin price, each contract is worth a certain amount of US dollars. This means if the contract is set to represent $1, the value in US dollars doesn’t change with the Bitcoin price. You know exactly how many dollars each contract represents.
Now, because each contract is worth a fixed amount of US dollars, the amount of Bitcoin you gain or lose from each contract changes as the price of Bitcoin changes. This is the “exponential” aspect.
For example, if the price of Bitcoin goes up, the same contract will represent less Bitcoin because each Bitcoin is worth more dollars. Conversely, if the Bitcoin price falls, that same contract will represent more Bitcoin because each Bitcoin is worth fewer dollars.
So, about the exponential part, to clarify once again. It doesn’t mean you’re getting an exponential return increase in a strict mathematical sense. Instead, it refers to the fact that your Bitcoin returns could significantly increase if the Bitcoin price falls, just as they could decrease if the Bitcoin price increases.
So, more returns in Bitcoin as the price falls, but less Bitcoin returns if the price goes up? Why would someone want that?
- Leverage & Hedging
Traders use these contracts to amplify their exposure to Bitcoin price movements. When the price of Bitcoin falls, if you’re holding a short position, the value of your position in terms of Bitcoin increases because each Bitcoin is now worth fewer US dollars.
This means you can buy back the contract at a lower Bitcoin price, which could give you more Bitcoin per dollar when you close your position. Conversely, if the price increases, your Bitcoin value decreases, but if you’re in a long position, you will profit.
Example for clarification
Inverse futures contracts have a non-linear nature. When we go long on the XBTUSD Perpetual contract inverse futures contract, we are essentially shorting USD. This is because the contract is inverse, which means that as BTC increases in value relative to the dollar, the worth of our position in BTC decreases.

Before

After
Please check the values and mark prices of future contracts. You will notice that the price of BTC has increased while the contract size, which is worth $1, has remained constant. However, the value of my long position in XBT has decreased.
The profits from holding BTC in your wallet give fewer gains in BTC as the value of BTC appreciates; however, the profits in USD are magnified.
Some investors, businesses, and institutions might hold Bitcoin and want to protect against the BTC price declines. By using inverse futures contracts, they can “lock in” the current dollar value of their Bitcoin holdings.
If Bitcoin’s price drops, the increase in Bitcoin returns from these contracts can offset the loss in value of their actual Bitcoin holdings. While they might not benefit from a rise in Bitcoin’s price, they won’t suffer a decline. In practical terms, if your BTC is deposited on BitMEX, you can use the inverse future contract and use 1x leverage short to “lock in” the dollar value.
There’s a reason why BitMEX calls dubbed their inverse futures contracts BitMEX hedging XBU series.
Here is a list with the inverse futures contract listed on BitMEX.
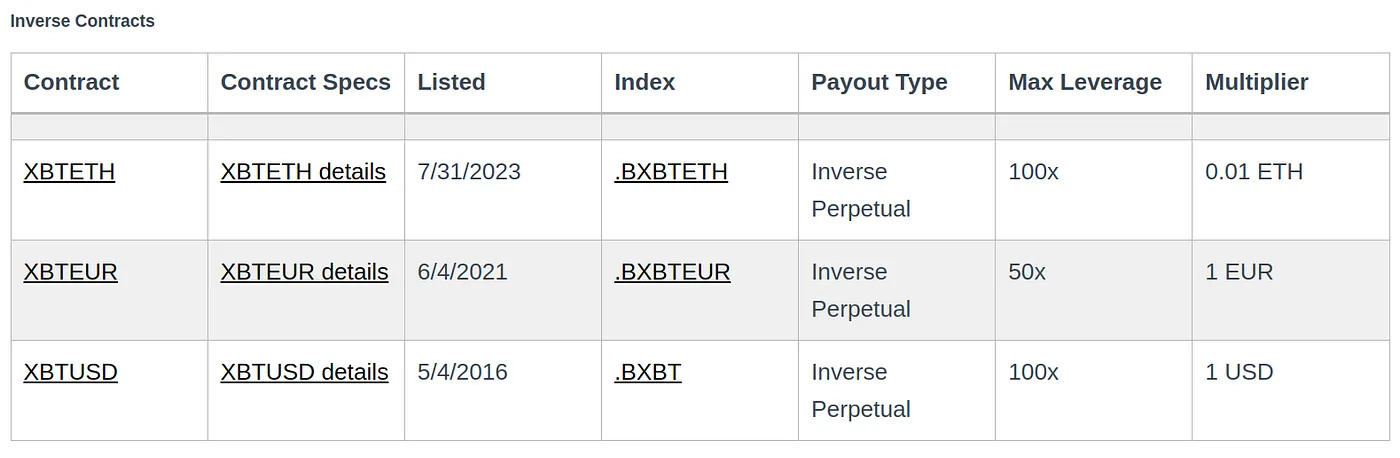
If you want to signup to BitMEX and want a 10% discount. You can use my referral link: https://www.bitmex.com/app/register/vhT2qm
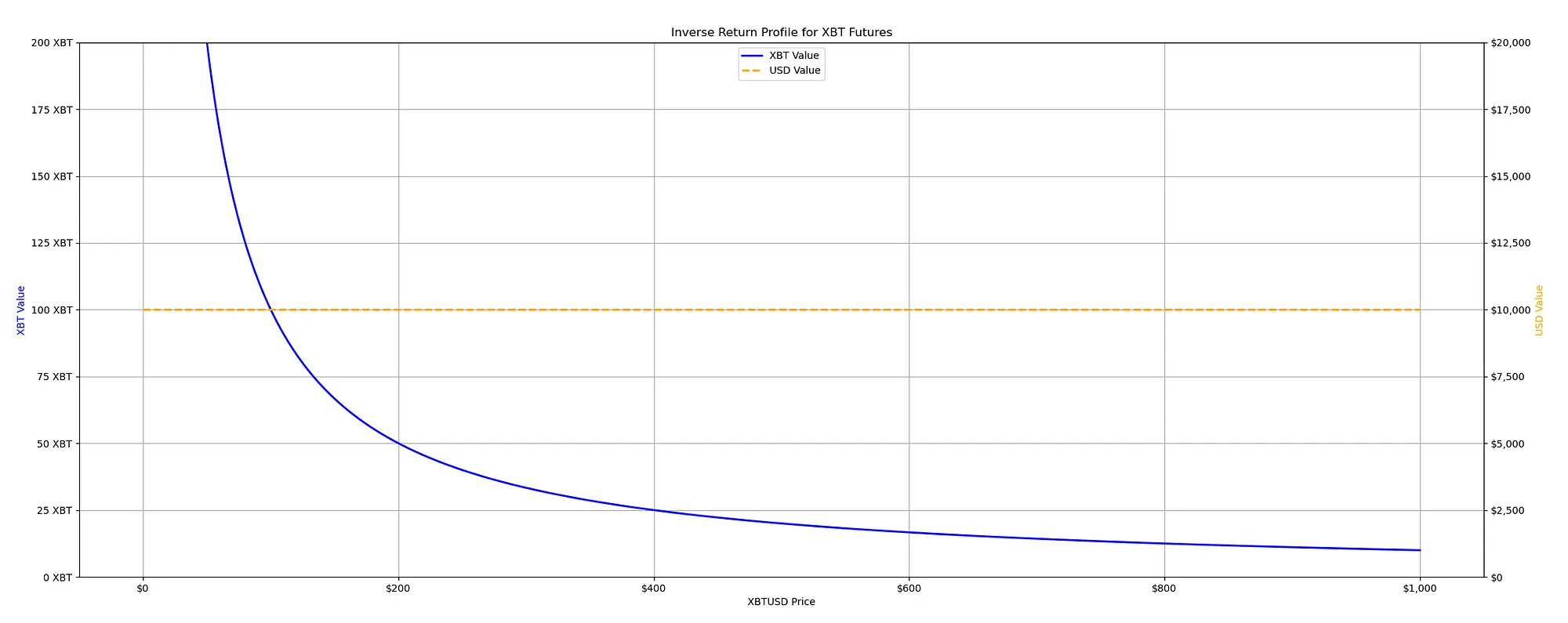
What does BitMEX XBTUSD Inverse Futures Return Profile Look Like?
As mentioned earlier, an “ inverse “ contract is a different kind of contract. Though it still deals with BTC/USD, its workings are flipped. Instead of your contact’s value being fixed in Bitcoin, it’s fixed in dollars. If the price of Bitcoin goes up, the same contract will represent less Bitcoin because each Bitcoin is worth more dollars. Conversely, if the Bitcoin price falls, that same contract will represent more Bitcoin because each Bitcoin is worth fewer dollars.
Now, you may wonder what that return profile looks like. Here is the XBTUSD perpetual contract specification. We see that the USD contract value is 1 USD.
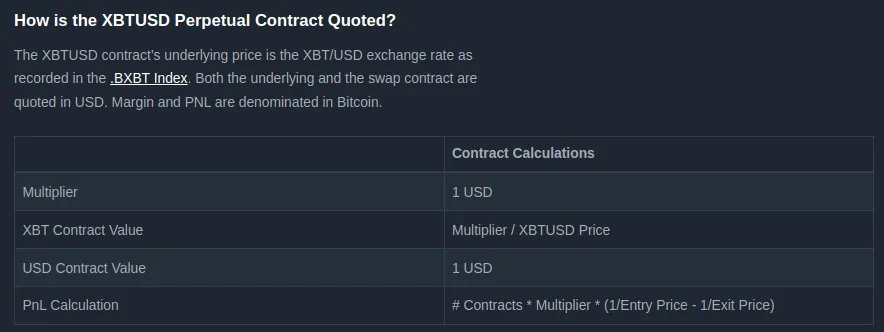
Compared to other cryptocurrency inverse contracts, such ETH inverse can have varying values in USD.
To provide ample illustration and ensure a thorough understanding, let’s consider a hypothetical scenario where the value of one contract is equivalent to $100.
If we have 100 futures contracts, each worth $100, the total value of our contracts in dollars is always $10,000, regardless of Bitcoin’s price.
Because they’re inverse contracts, when the price of Bitcoin goes down, the amount of BTC that each of our contracts is worth goes up. You know, because we could buy more BTC in dollars if the price of BTC is lower. On the other hand, if the price of Bitcoin goes up, the amount of BTC you get per contract goes down. This is why we say the Bitcoin value is ‘exponential’ or follows a ‘1 over x’ pattern, as shown by the asymptotic curve in the graph.
Source code for the python script to generate this graph: https://github.com/romanornr/bitmex_pnl_model/tree/main/inverse_futures
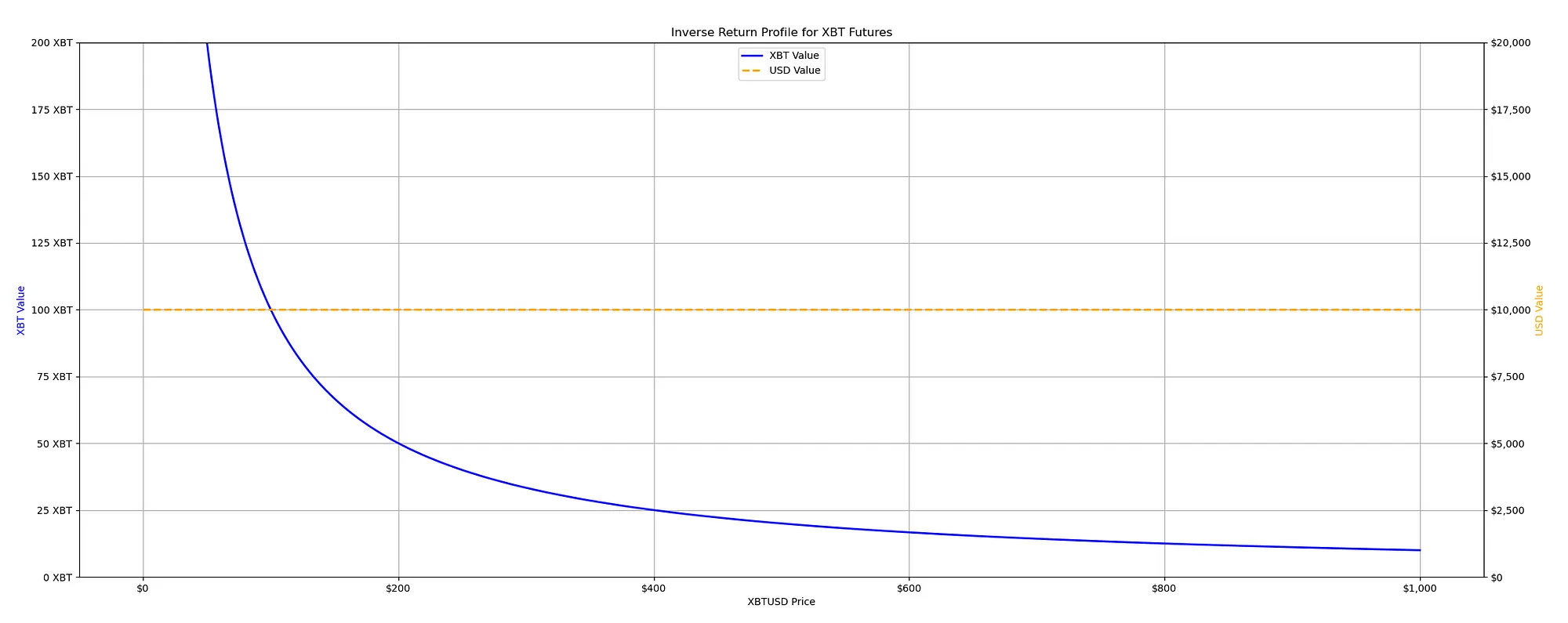
As Bitcoin’s price falls, the horizontal axis gets closer and closer to it but never actually touches out. In the best-case scenario, our potential profit is that you can only double your money or get a 100% return on these inverse contracts if you go long.
However, if the price of Bitcoin goes down, the graph shows that the Bitcoin value of our contracts could increase without a limit. This is because, mathematically, as you divide by a smaller and smaller number (the price of Bitcoin, which is getting lower), the results get larger and larger.
BitMEX Quanto Futures vs. Inverse Futures
Let’s figure out what is better suited for what type of trader.
Quanto futures contracts on BitMEX appeal to traders with a bullish view or those who want to speculate in Bitcoin instead of the dollar. What makes Quanto Futures unique is its ability to speculate on a range of assets such as Ethereum, Link, Avax, Solana, Aptos, SUI, and Dogecoin and their price movements against USDT with margins posted in BTC.
The settlement of these contracts is in Bitcoin (XBT), not the USDT or the underlying asset (ETH, LINK, SOL, APT, SUI). This design allows traders to speculate on the price movements of underlying assets in USDT while holding only Bitcoin.
Another advantage of Quanto futures contracts for bullish speculators is that they typically trade at a premium (contango), especially when the market sentiment is bullish, and offer a higher return.
On the other hand, inverse futures contracts are designed for ‘bearish traders’ who want to hedge the value of BTC against the U.S. dollar. These contracts work inversely to traditional linear futures; as the price of BTC calls increases, the contract’s value in USD increases, allowing traders to profit from downward market movements.
Reminder: When trading Linear futures contracts, you need to deposit USDT as collateral, and your margin and PNL will also be in USDT. In order to trade linear futures on BitMEX, you are required to deposit USDT.
For investors holding BTC but concerned about a potential fall in its price, inverse futures contracts are an attractive hedging tool. By entering into an inverse futures contract, traders can lock in a price for Bitcoin and protect themselves against price declines. It’s a great tool to know about, especially since the market tends to be volatile.
Now let’s consider a scenario in which the price of Bitcoin in US dollars is set at $500. We’re working with BitMEX quanto futures and inverse futures, which depict the return profiles of holding 4000 contracts with an initial entry price of $500.
For both contract types, we see the PNL in Bitcoin and US dollar terms over a range of Bitcoin prices from $0 to $1000. The Profit and Loss (PNL) for both types of contracts is visually illustrated in terms of Bitcoin and US dollar.
Source code to generate this PNL graph: https://github.com/romanornr/bitmex_pnl_model/tree/main/quanto_vs_inverse
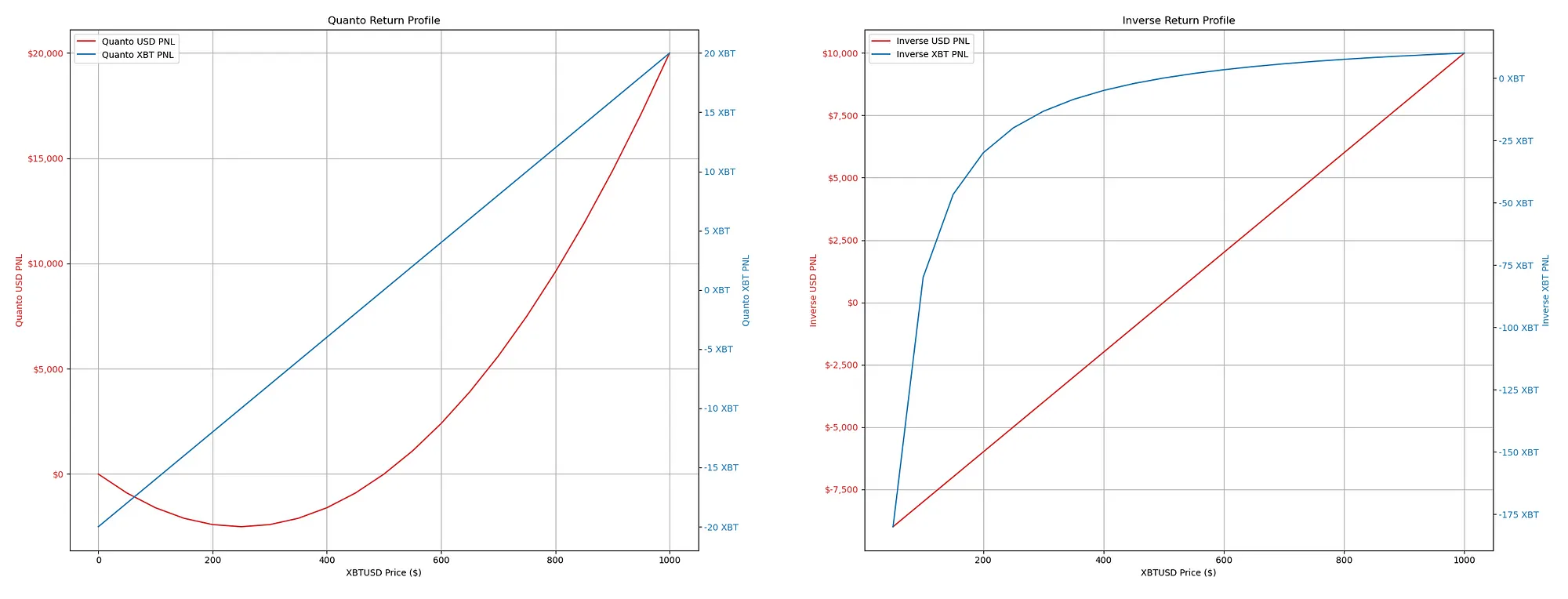
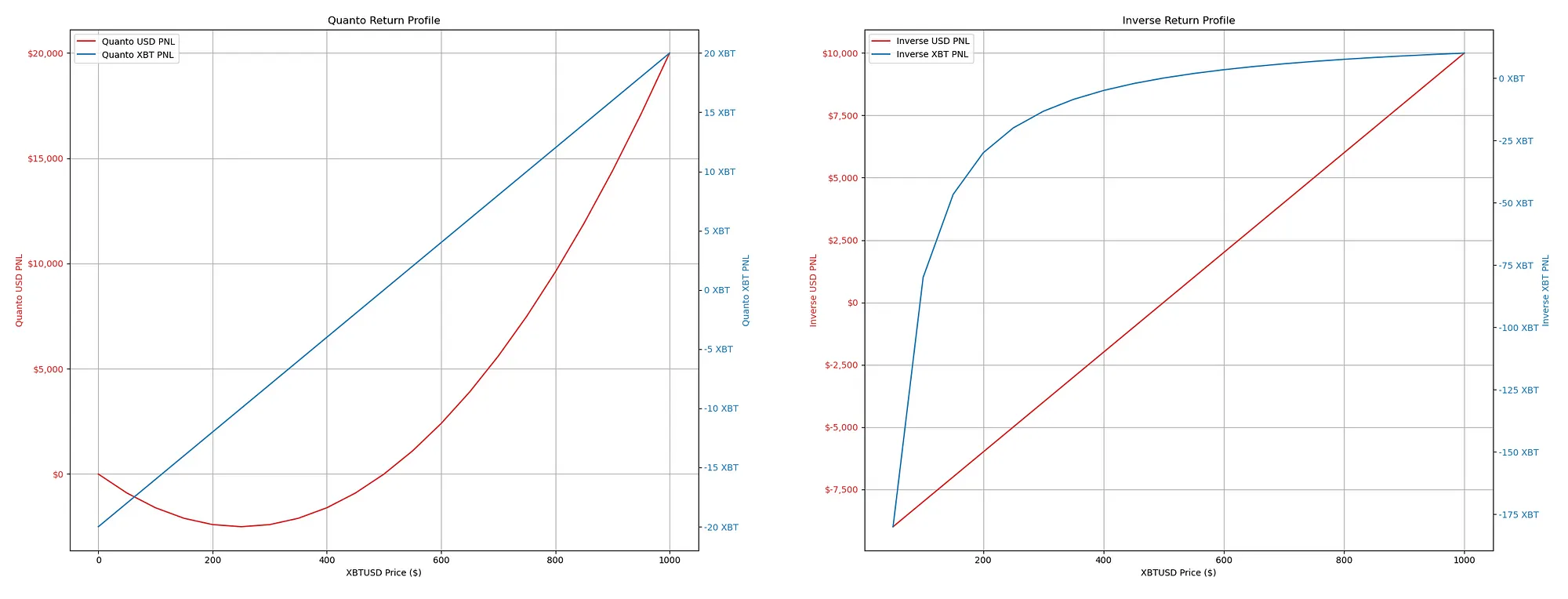
Quanto Futures Return Profile
- We are at the entry point at a bitcoin price of $500, so the PNL for both USD and XBT is around zero.
- As Bitcoin’s price goes above the entry price of $500, the Quanto USD PNL (red line) increases, which occurs at an accelerating rate. This means that as the Bitcoin price keeps rising, the profits in USD terms become increasingly larger. By holding a quanto futures position, you can make more profits in USD as the Bitcoin price increases and the profit growth rate also accelerates. This is because quanto futures use a payoff structure that multiplies the Bitcoin price increases.
- When the price of Bitcoin drops below the entry price, the US dollar profit and loss (PNL) also decreases. However, the decrease in PNL becomes less steep and even flattens as the Bitcoin price approaches zero. It’s important to note that losses can occur when the Bitcoin price falls below the entry price, but they may decrease slower than gains when the price goes up. In other words, losses in USD terms are not as sensitive to the price of Bitcoin falling as the gains are when the Bitcoin price rises.
The convex return profile in USD PNL for the quanto futures shows that the contract can be structured so that the PNL, in USD terms, benefits from a rising Bitcoin price relative to losses from a falling Bitcoin price.
The asymmetry of Bitcoin futures appeals to traders who want to take advantage of the cryptocurrency’s potential for gains while minimizing their exposure to USD losses. However, it’s important to note that losses are not entirely eliminated, and Quanto futures may trade at a premium.
Inverse Futures Return Profile
- The inverse USD PNL shows a linear relationship with the price of Bitcoin. For every dollar change in the price of bitcoin, the profit or loss in USD terms changes by a constant amount.
- As the price of Bitcoin increases from an entry price of $500, the USD PNL falls linearly.
- The XBT PNL shows a non-linear relationship with the price of Bitcoin. When the price rises above the entry price, the PNL in Bitcoin increases; each contract represents a smaller amount of Bitcoin since the payout is in USD, and each USD buys less BTC as the price rises). The profit in Bitcoin terms grows, but each additional dollar represents a smaller fraction of Bitcoin.
- When the price of Bitcoin drops below $500, the losses are accelerated because the decreasing price means that each lost dollar represents a greater amount of Bitcoin.
- The PNL in Bitcoin (blue line) has a non-linear relationship with the price of Bitcoin. It increases with the price of Bitcoin but at a decreasing rate, suggesting a form of hedging by reducing exposure in Bitcoin terms as the price of Bitcoin increases.
Long Quanto vs. Short Inverse Postion
Let’s make two bets on the price of Bitcoin with different payouts depending on the direction of the price movement. Our analysis will consider Bitcoin’s price range from $0 to $1000.
We are interested in the Quanto future, a type of bet that allows us to earn more U.S. dollars if the underlying asset’s price, bitcoin (BTC), increases. The payout of a quanto contract is based on the percentage change in the asset’s price but calculated in another currency, in this case, the dollar. Therefore, as the price of Bitcoin goes up, the potential profits in USD also increase at an accelerating rate.
On the other hand, a ‘Short inverse’ position is essentially a bet against the price. In this position, we earn a profit if the price falls, but we use the ‘inverse future contract’ to bring that bet to life. The profit or loss (P&L) for this strategy is reflected in Bitcoin. As the price of Bitcoin increases, the contract loses value rapidly due to its ‘inverse’ nature, as explained earlier. The ‘inverse futures contract’ payout structure is a function of the reciprocal of the asset price. However, since we are short, we gain more USD as the price of Bitcoin drops.
Source code to generate this graph: https://github.com/romanornr/bitmex_pnl_model/tree/main/quanto-inverse-combination
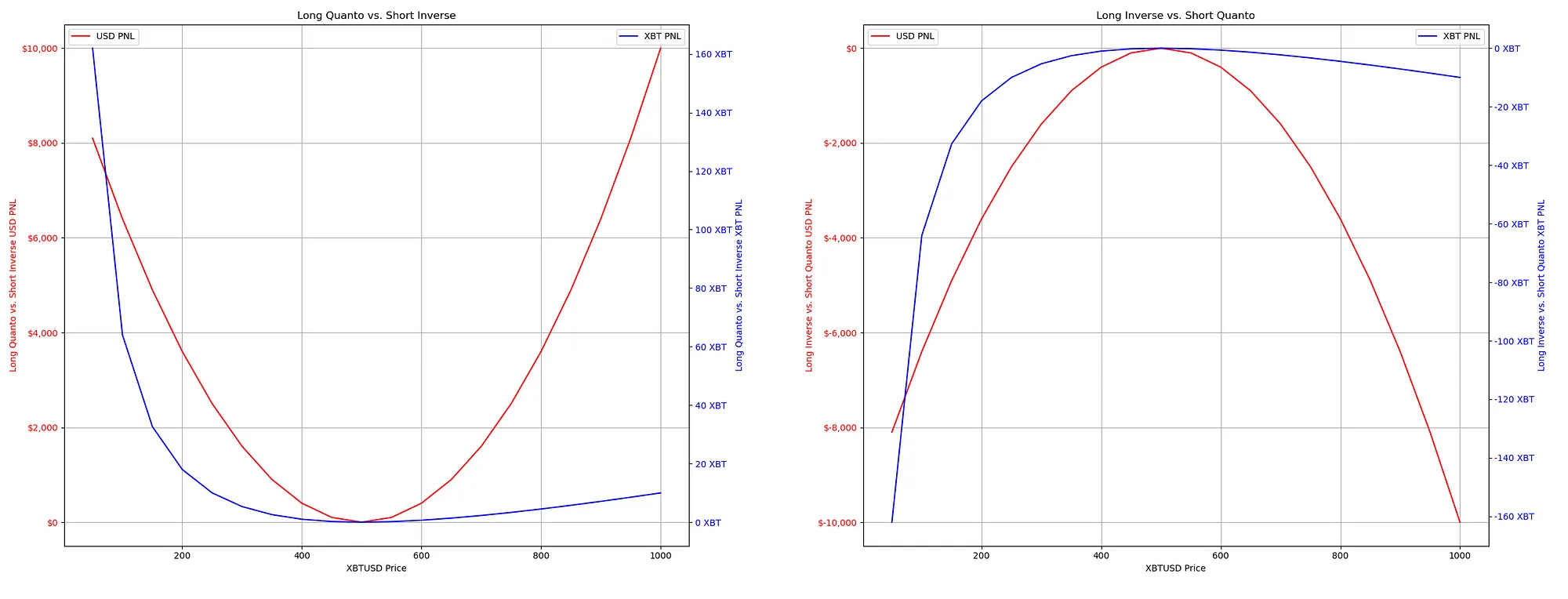
When these two positions work together, they create a dual-benefit scenario. If the price of Bitcoin increases, our long quanto position should yield a squared return in dollars due to the magnifying effect of the quanto futures contract. On the other hand, if the price falls, our short inverse position should be profitable, as it is designed to hedge and benefit from a falling market.
This approach takes advantage of volatility, allowing us to profit whether the price skyrockets or nosedives without accurately predicting its direction but the magnitude of the direction.
This may remind you of a long straddle 😉 // TODO Needs context
You need to know how the Bitcoin value of your contracts changes with the change in price because BitMEX margins their futures contracts in Bitcoin. When you’re trading with a long Quanto and short inverse combination, the inverse futures are the contracts that will increase in their Bitcoin-denominated value when the dollar price of Bitcoin falls. The Bitcoin-denominated value falls when the price rises.
Due to these fluctuations, It is possible that you may need to deposit extra Bitcoin into your margin account at times due to fluctuations in the market. This extra margin is necessary to meet the maintenance requirements and ensure that you can uphold your trades despite significant price swings. It is important to remain vigilant of market changes to manage your margins effectively and avoid liquidation.
Here’s a list of Quanto futures trading on BitMEX: https://www.bitmex.com/app/contractList#Quanto-Futures
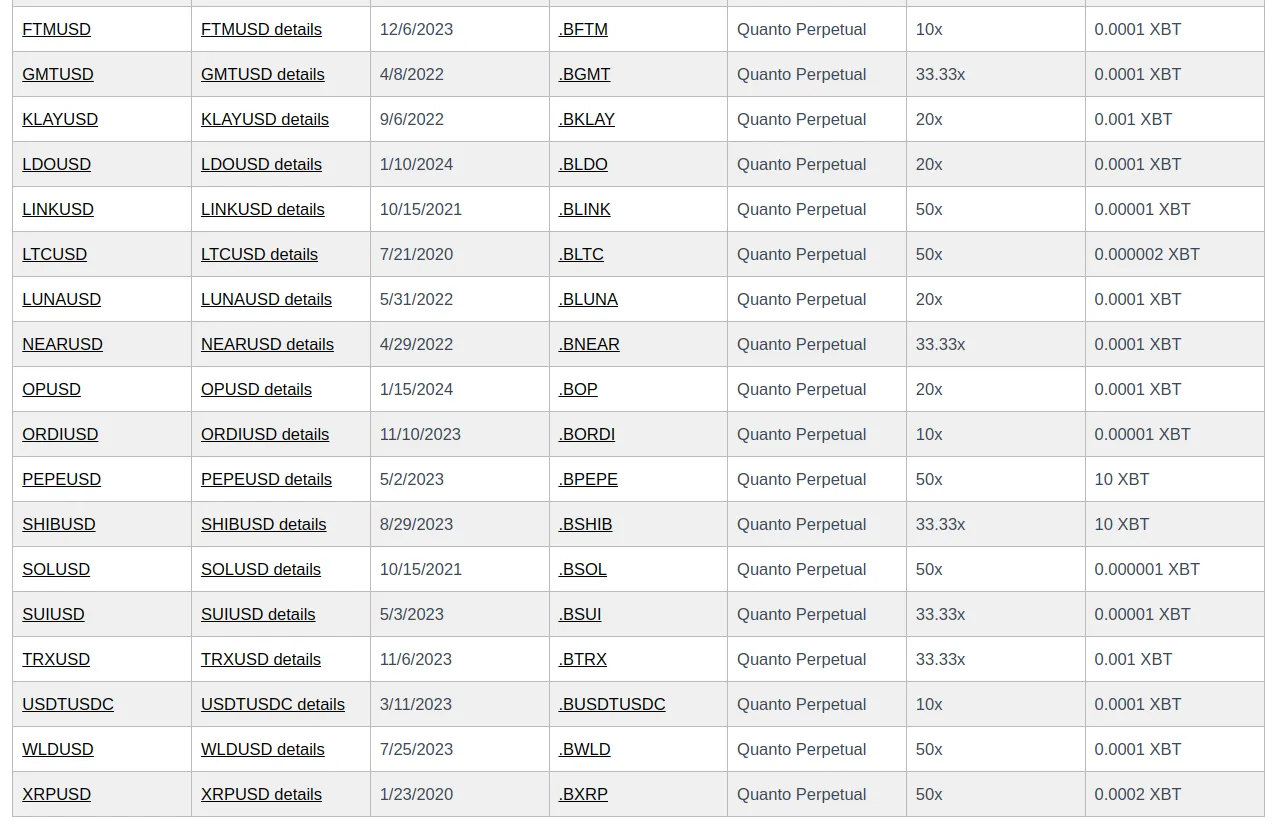
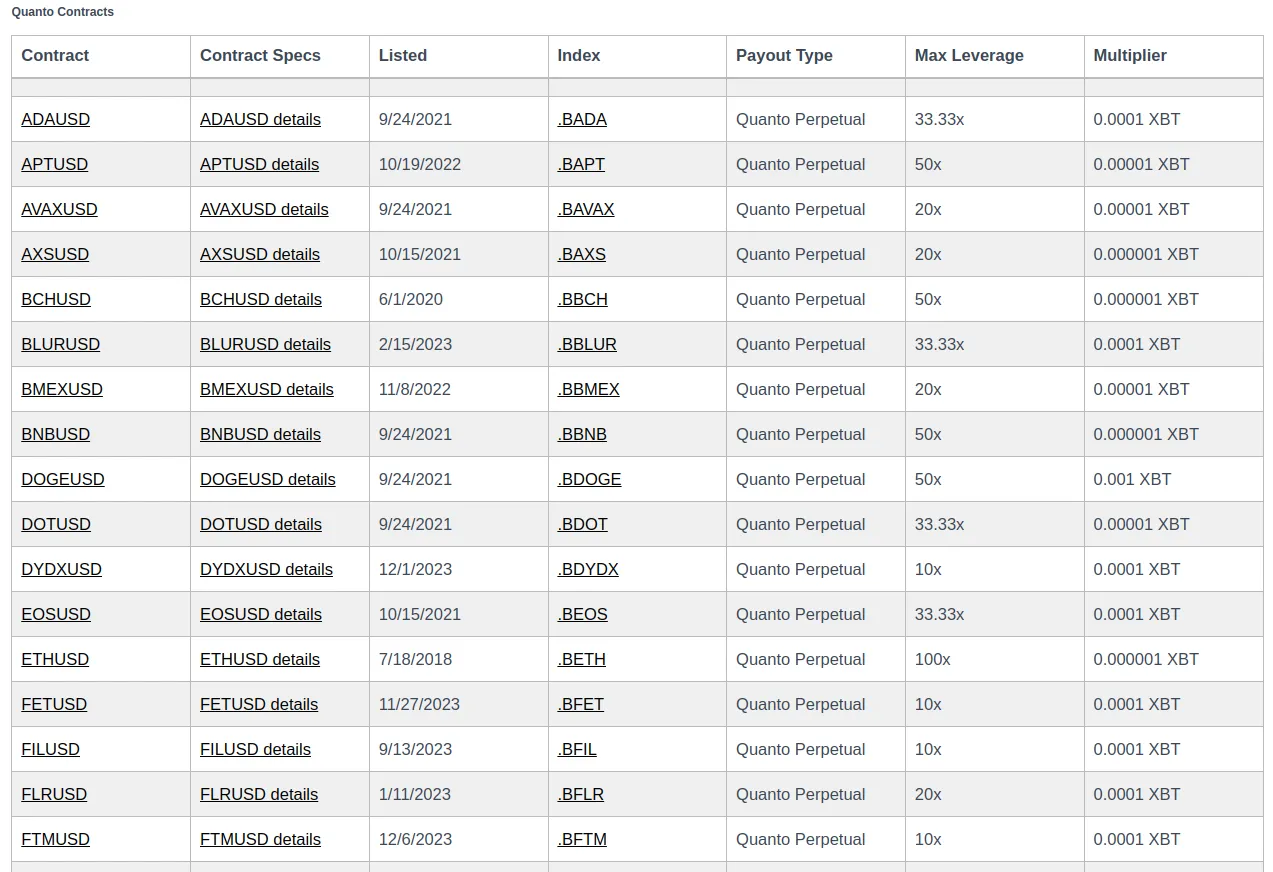
Again, the list of Quanto futures on BitMEX is much larger, and you can find the full list here: https://www.bitmex.com/app/contractList#Quanto-Futures
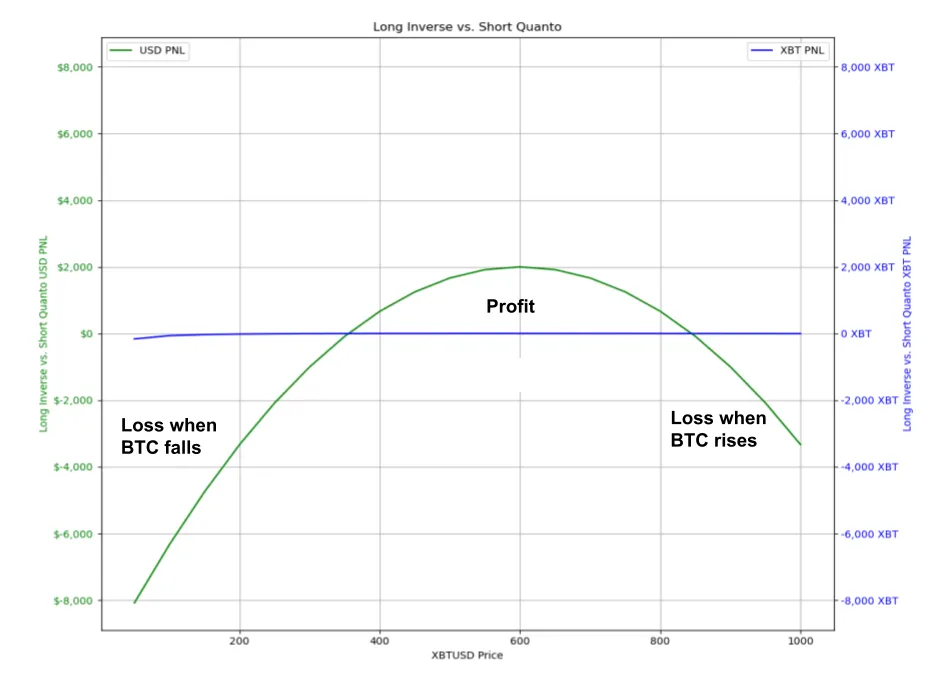
Long Inverse and Short Quanto Combination Position
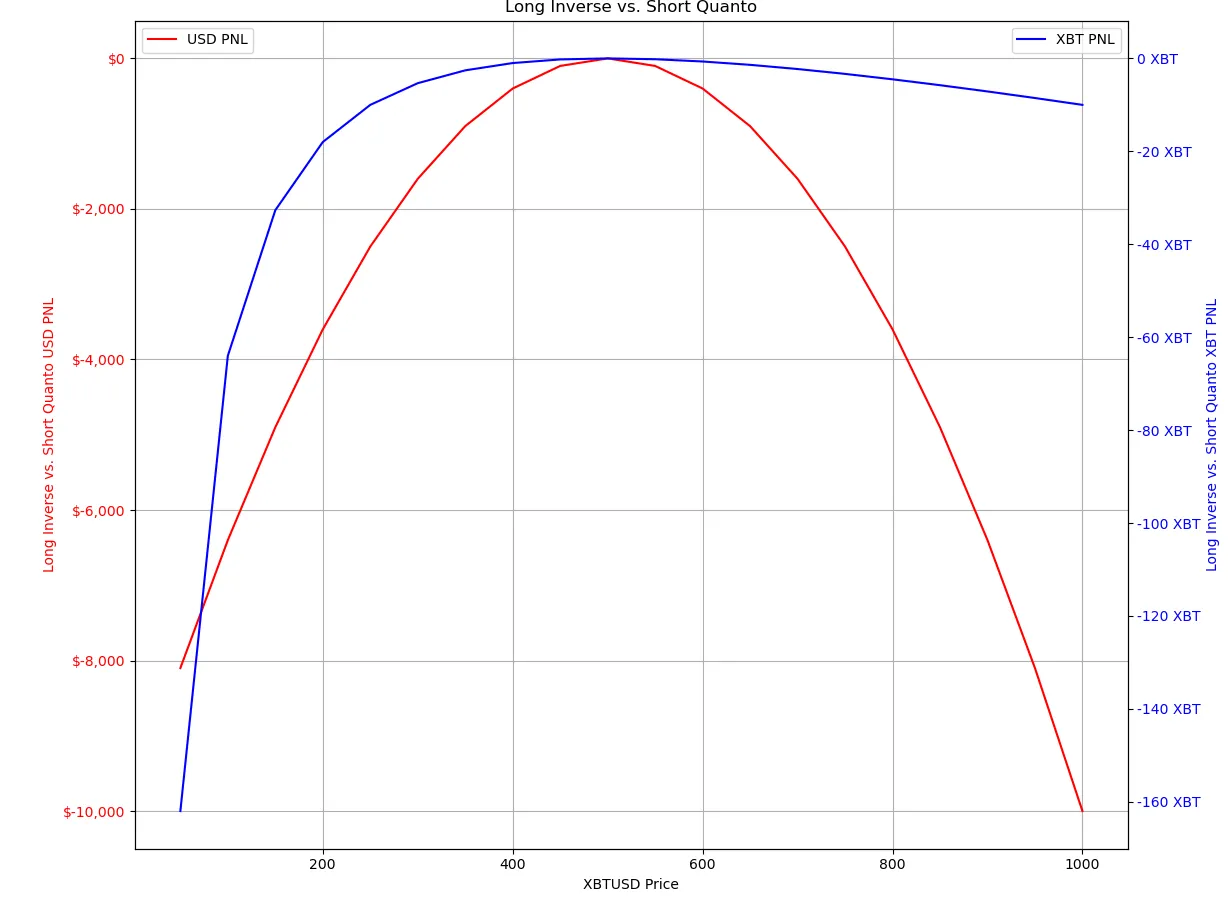
Now let’s look at the opposite; let’s make two bets on the price of Bitcoin. We long the “inverse futures contract” and “short quanto contract.” Our analysis will consider Bitcoin’s price range from $0 to $1000.
In the “long inverse and short quanto scenario,” the graph presents a mirrored parabola, indicating that our P&L outcome is predominantly negative regardless of whether the Bitcoin price goes up or down.
Just a heads up, the parabolic effect of both “long quanto & short inverse” and “long inverse & short inverse” is comparable to “gamma” in options trading and “convexity” in bond trading. To learn more about gamma, read this article by Romano RNR.
Gamma refers to the rate of change in the delta of an option, while convexity refers to the sensitivity of a bond’s duration to changes in interest rates.
Both terms describe a situation where the returns are non-linear, meaning that the changes in price become more significant as we move toward the extremes.
In the case of “long inverse & short quanto,” this non-linear relationship exposes us to increased risk. If the price moves drastically in either direction, our Profit and Loss (P&L) can deteriorate quickly.
Holding a long position in a quanto contract while being short in an inverse contract can be advantageous. However, it is important to note that these contracts may not be priced equally or “fair” at all times.
Usually, a quanto contract carries a “premium” due to the additional risks and payoff it presents.
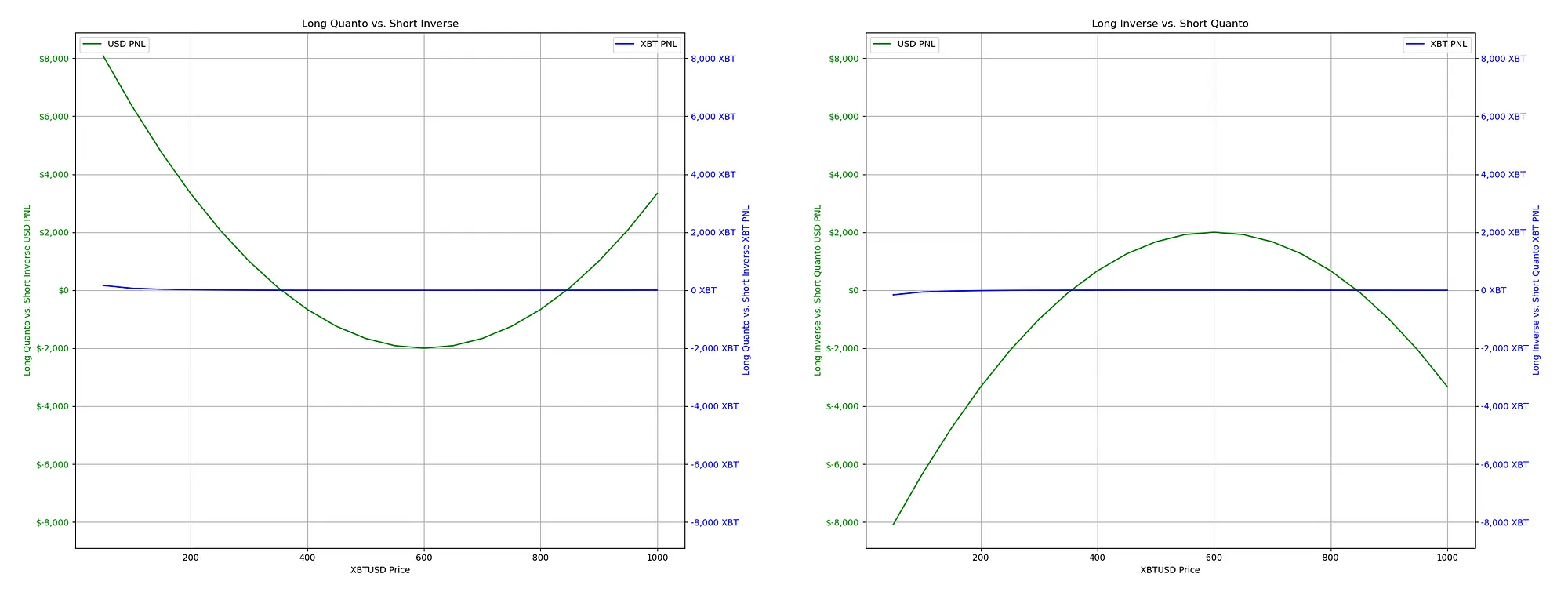
For the purpose of our analysis, let’s assume this premium is $100. This adjustment shifts the P&L graphs, reflecting the premium it costs to enter the long quanto position.
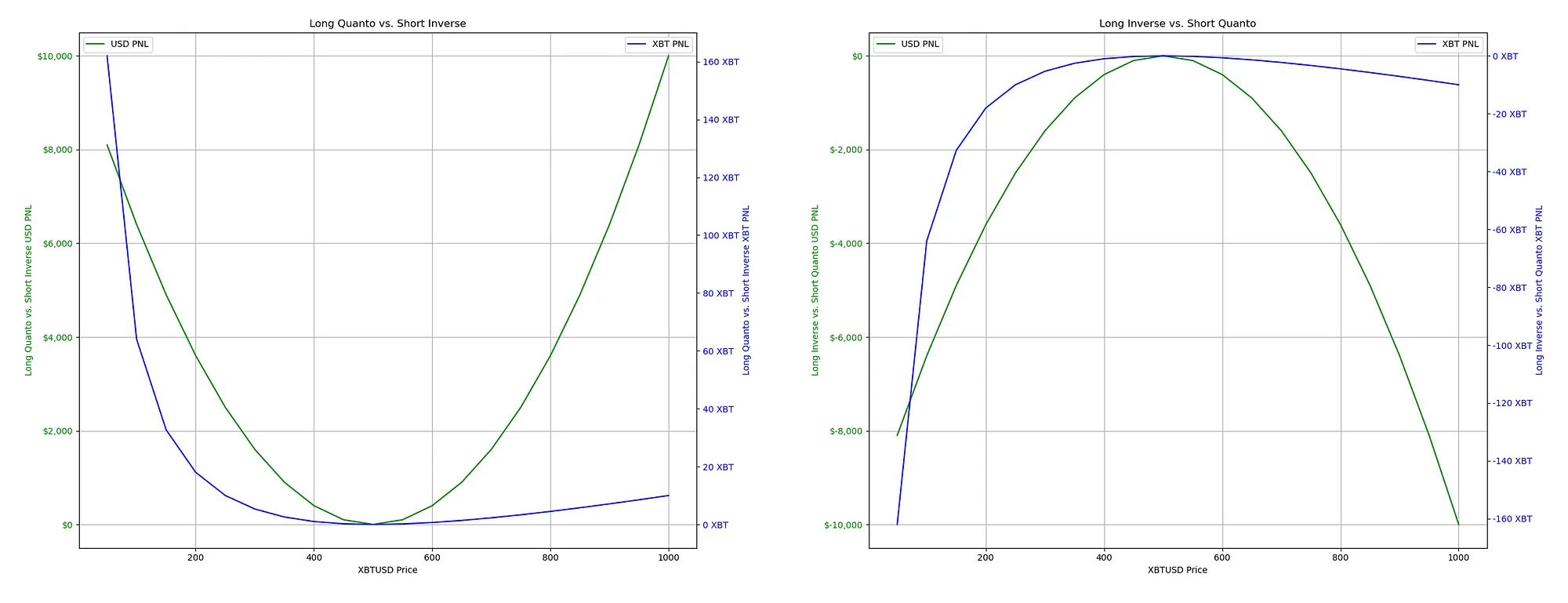
In a “Long Quanto vs. Short Inverse” setup, we are entering a derivatives position sensitive to Bitcoin’s price movements and the corresponding impact on the USD payout, which depends on both the BTC price and its volatility.
When we take a long position in a quanto contract, we expose ourselves to a non-linear payoff profile. This means that our profit and loss (P&L) is not a straightforward function of the Bitcoin (BTC) price, like a linear contract. Instead, the effect of the BTC price is squared due to the quanto feature. In simpler terms, if the price of BTC moves significantly in either direction, our USD return will increase exponentially.
Although the enhanced exposure has benefits, it comes at a cost, which is reflected as a premium over the short inverse contract. This premium essentially represents the market’s future implied volatility expectations, and the implied volatility is priced into the contract. When we pay this premium, we’re betting on volatility greater than what the market expects.
If the market experiences more volatility compared to what it expects priced into the quanto premium, the premium we paid for the long quanto position may erode our potential profits. This “erosion” is called “time decay” or “theta,” a concept borrowed from options trading. The position’s value erodes over time as it approaches the expiration date. To learn more about time decay and theta, read this article by Romano RNR.
After incorporating the $100 premium, we see the risk zone where our position is “underwater.” This means the market price would need to move significantly in either direction for us to break even and cover the cost of the quanto premium. This is similar to an “options premium,” where you need the market to move enough to compensate for the premium you initially paid.
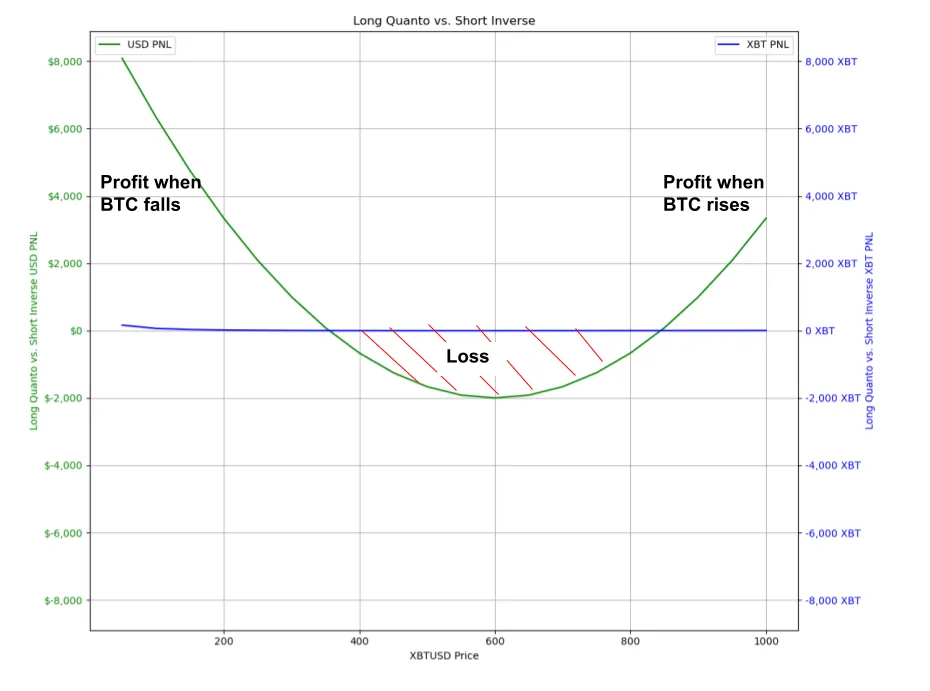
If we were to take the opposite position, selling volatility by going “Long inverse and short quanto,” we would collect a premium similar to an option seller. We would profit as long as the market stays within the range, but the risk is that if the BTC price moves beyond this range, our losses increase in a non-linear fashion due to the short position in the quanto contract.
Is it Better to Always Be Long Quanto and Short Inverse?
It is not always the best choice to be long quanto and short inverse, even though it may sound like the better option. The decision depends heavily on the cost associated with entering the trade, which is the expected volatility priced into the quanto premium and your predictions for future market volatility.
It’s basically an assessment of the market’s implied volatility (IV) and realized volatility (RV). When you long a quanto contract, you’re buying implied volatility. If the market’s future realized volatility ends up being lower than the implied volatility priced into the Quanto contract, then the premium was not worth it. It’s like buying a ticket for a festival, but the event didn’t live up to the hype, and the “ticket” was overpriced.
Conversely, if the implied volatility is low relative to the potential high realized volatility we expect, and the realized volatility ends up being higher than what the market expected, then having a “long quanto vs. short inverse” position could be very profitable without much directional exposure.
If the quanto premium is too high and we don’t think that the market will experience enough volatility to justify that premium, then it’s better to take the opposite position. This means going “Long Inverse and Short Quanto,” which is similar to being the “seller” of volatility. In this position, we can profit if the volatility turns out to be lower than what the market expected. So, if the market does not move as much as the Quanto premium, we can still make a profit.
Understanding market sentiment, derivative pricing, and risk management is key to trading with historical and implied volatility analysis.
If you want to signup to BitMEX and want a 10% discount. You can use my referral link: https://www.bitmex.com/app/register/vhT2qm
What’s the Point of All of This?
In October/November 2020, I stumbled upon an old article about BitMEX. It mentioned the term “convexity,” which piqued my interest. That same day, I began researching more about the topic by using Google to find additional information.
Maybe you’re not interested in Bitcoin trading, but rather altcoins. If so, you’ll love trading on BitMEX. Stick with me till the end for more information about applying everything you’ve learned to trade altcoins and supercharge your P&L
Read the article on convexity by Arthur Hayes here.
On that same day, I learned about options trading and terms such as “convexity squeeze” and “gamma squeeze.” Before the Gamestop gamma squeeze, a gamma squeeze was happening in Tesla, which I tried to ‘study.’
The word “convexity” changed everything for me since. It was probably the most pivotal moment.
So about these contracts and their complexity. Convexity, also known as “Gamma,” measures how sensitively a derivative’s value changes as the price of the underlying asset changes.
It’s like the acceleration of a car; it’s not just about how fast you’re going (like the delta, also known as the first derivative) but how quickly that speed is increasing.
Convexity can amplify your portfolio gains. You can make larger profits if the market swings in your favor beyond what you accounted for by the first-order price movement, which is the delta.
However, if you don’t understand convexity and how it affects the derivatives you’re trading, you won’t be able to account for how rapidly your position’s value can change, and you risk repeatedly being financially destroyed.
When not understood or mismanaged, your losses will compound non-linearly.
So, the BitMEX XBTUSD perpetual swap has always been an “inverse futures contract,” and many have traded that in the past. Did you know that? It’s a shocker for some.
The same goes for Deribit. Those were always “inverse futures contracts” and many contracts on OkEx.
What did we learn about inverse futures contracts again?
- Inverse futures are contracts that increase in their Bitcoin-denominated value when the dollar price of Bitcoin falls, and the Bitcoin-denominated value falls when the price rises.
- This is why we say the Bitcoin value is ‘exponential’ or follows a ‘1 over x’ pattern, as shown by the asymptotic curve in the graph.
- Inverse futures contracts are designed for ‘bearish traders’ who want to hedge the value of BTC against the U.S. dollar. These contracts work inversely to traditional linear futures; as the price of BTC calls increases, the contract’s value in USD increases, allowing traders to profit from downward market movements.
- When you long an “inverse futures contract”, the losses are accelerated because the decreasing price means that each lost dollar represents a greater amount of Bitcoin.
Yes, the XBTUSD perpetual swap has always been an “inverse futures contract,” and many have traded that in the past to long Bitcoin. Ironically, these contracts are meant for hedging, not speculating.
If you’re bullish, don’t use the “inverse futures contracts” but the “Quanto futures contracts,” and if that isn’t available, use the “linear futures contracts.”
BitMEX Linear futures list can be found here.
Reminder: When trading Linear futures contracts, you need to deposit USDT as collateral, and your margin and PNL will also be in USDT. In order to trade linear futures on BitMEX, you are required to deposit USDT.
If you are bearish or want to hedge your exposure, use the “inverse futures contracts.”
BitMEX Inverse futures list can be found here: https://www.bitmex.com/app/perpetualContractsGuide#Inverse-Contracts
Linear futures contracts weren’t available in the early days due to regulations. Trading them exposes you to Tether, which some consider risky.
Instead of selling BTC, you can deposit it on Bitmex and hedge by shorting XBTUSD with 1x leverage, creating a synthetic USD position. By opening a 1x short position on XBTUSD inverse, you can earn some extra passive income due to the funding rate if it’s in your favor.
What About Quanto Futures for Altcoin Trading?
If you are bullish on BTC and altcoins, you can trade BitMEX Quanto futures for altcoins and amplify your PNL non-linearly. On top of that, your PNL will be in BTC, adding another layer of speculation.
Now that you have learned about quanto futures contracts, you can use this knowledge in practical scenarios.
For instance, if you are holding a long position on an altcoin with a quanto futures contract and you notice that BTC is underperforming while the altcoin is bullish, you can keep your Quanto long position on the altcoin open and use the “inverse future contract XBTUSD” to short your BTC exposure. This will help to hedge efficiently.
BitMEX Quanto futures list including altcoins can be found here.
These days, you can also deposit Ethereum on Bitmex, and they have an inverse futures contract for Ethereum in case you need to hedge: https://www.bitmex.com/app/trade/XBTETH
You can apply what you’ve learned and shorten the inverse futures contract for Ethereum while opening a long Quanto position on Ethereum. Or, if you believe the Quanto premium is too high and volatility turns lower than expected, you can short Quanto and long inverse.
You can find the Quanto contract for Ethereum here.
I recommend using BitMEX Testnet to practice what you’ve learned.
If you want to signup to BitMEX and want a 10% discount. You can use my referral link: https://www.bitmex.com/app/register/vhT2qm
